Optimización del precio del producto mediante regresión

Muy buenas, soy Miguel y aquí les traigo este tutorial.

El precio y la cantidad son dos medidas fundamentales que determinan el resultado final de cada negocio, y establecer el precio correcto es una de las decisiones más importantes que puede tomar una empresa.

La subvaloración perjudica los ingresos de la empresa si los consumidores están dispuestos a pagar más y, por otro lado, la sobrevaloración puede afectar de manera similar si los consumidores están menos inclinados a comprar el producto a un precio más alto.

Entonces, dada la complicada relación entre precio y ventas, ¿dónde está el punto óptimo, el precio óptimo, que maximiza las ventas de productos y obtiene la mayor ganancia?

El propósito de este artículo es responder a esta pregunta implementando una combinación de la teoría económica y un algoritmo de regresión en el entorno de Python.

1. Datos

Estamos optimizando un precio futuro basado en la relación entre el precio histórico y las ventas, por lo que lo primero que necesitamos son los datos pasados ​​de estos dos indicadores.

Para este ejercicio, estoy usando datos de series de tiempo sobre ventas de carne vacuna y precios unitarios correspondientes.

# load data
import pandas as pd
beef = pd

# view first few rows
beef.tail(5

El conjunto de datos contiene un total de 91 observaciones de pares cantidad-precio reportados trimestralmente.

Es habitual en la ciencia de datos hacer análisis de datos exploratorios (EDA), pero me salto esa parte para centrarme en el modelado. No obstante, le recomiendo encarecidamente que realice este paso adicional para asegurarse de que comprende los datos antes de crear modelos.

2. Bibliotecas

Necesitamos importar bibliotecas por tres razones: manipular datos, construir el modelo y visualizar las funciones.

Nosotros importamos numpy y pandas para crear y manipular mesas, mtplotlib y seaborn para visualización y statsmodels API para construir y ejecutar el modelo de regresión.

import numpy as np
from pandas import DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.formula.api import ols
%matplotlib inline

3. Definición de la función de beneficios

Sabemos que los ingresos dependen de la cantidad vendida y del precio unitario de los productos.

También sabemos que las ganancias se calculan deduciendo los costos de los ingresos.

Poniendo estos dos juntos obtenemos las siguientes ecuaciones:

# revenue
revenue = quantity * price # eq (1)

# profit
profit = revenue - cost # eq (2)

Podemos reescribir la función de ganancias combinando la ecuación. # 1 y 2 de la siguiente manera:

# revised profit function profit = quantity * price - cost # eq (3)

La ecuación # 3 nos dice que necesitamos tres piezas de información para calcular la ganancia: cantidad, precio y costo.

4. Definición de la función de demanda

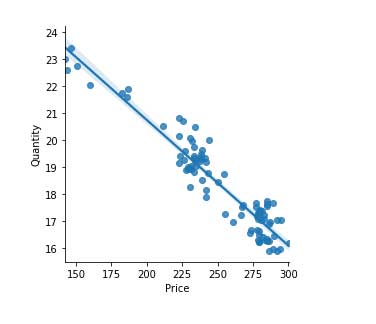
Primero necesitamos establecer la relación entre cantidad y precio: la función de demanda. Esta función de demanda se estima a partir de una "curva de demanda" basada en la relación lineal entre precio y cantidad.

# demand curve
sns.lmplot(x = "Price", y = "Quantity", 
data = beef, fig_reg = True, size = 4)

Para encontrar esa curva de demanda, ajustaremos un modelo de regresión de mínimos cuadrados ordinarios (MCO).

# fit OLS model
model = ols("Quantity ~ Price", data = beef).fit()

# print model summary
print(model.summary())

Los siguientes son los resultados de la regresión con los coeficientes necesarios para un análisis más detallado.

5. Encontrar el precio que maximiza las ganancias

El coeficiente que estamos buscando proviene del modelo de regresión anterior, la intersección y el coeficiente de precio, para medir la cantidad de ventas correspondiente.

Ahora podemos insertar estos valores en la ecuación 3.

# plugging regression coefficients
quantity = 30.05 - 0.0465 * price # eq (5)

# the profit function in eq (3) becomes
profit = (30.05 - 0.0465 * price) * price - cost # eq (6)

El siguiente paso es encontrar el precio que estamos buscando entre una variedad de opciones.

Los códigos a continuación deben ser intuitivos, pero básicamente lo que estamos haciendo aquí es calcular los ingresos por cada precio y la cantidad correspondiente vendida.

# a range of diffferent prices to find the optimum one
Price = [320, 330, 340, 350, 360, 370, 380, 390]

# assuming a fixed cost
cost = 80

Revenue = []

for i in Price:
quantity_demanded = 30.05 - 0.0465 * i

     # profit function
     Revenue.append((i-cost) * quantity_demanded)

# create data frame of price and revenue
profit = pd.DataFrame("Price": Price, "Revenue": Revenue)

#plot revenue against price
plt.plot(profit["Price"], profit["Revenue"])

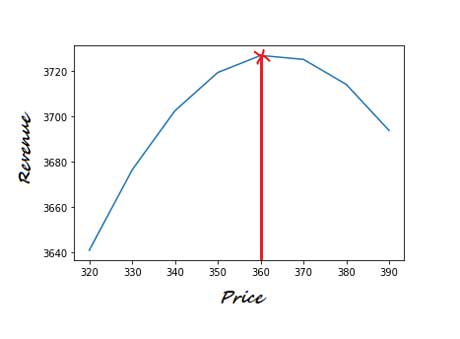
Si se grafican el precio y los ingresos, podemos identificar visualmente el pico de los ingresos y encontrar el precio que genera los ingresos en el punto más alto de la curva.

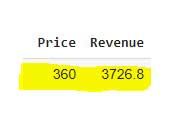
Entonces, encontramos que los ingresos máximos a diferentes niveles de precios se alcanzan en $ 3,726 cuando el precio se establece en $ 360.

# price at which revenue is maximum
profit[profit['Revenue'] == profit[['Revenue'].max()]

Gracias por leer este tutorial.