Bienvenido, les saluda Miguel y aquí les traigo un nuevo tutorial.
En el artículo anterior, decidimos analizar e implementar Bubble Sort. En el artículo de hoy, vamos a echar un vistazo a un algoritmo de clasificación mejor conocido como Ordenación por inserción y veremos cómo funciona bajo el capó.
Los archivos XCode Playground con implementaciones están disponibles en este enlace.
¿Qué es el ordenamiento por inserción?
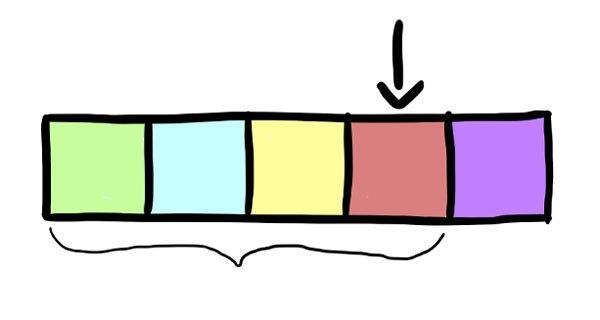
Insertion Sort se inspira en la forma en que clasificaría una mano de cartas barajadas. Empieza por la segunda carta y la compara con la primera carta. Si la segunda carta es más pequeña, la desplaza sobre un lugar a la izquierda, de lo contrario la deja y pasa a la tercera carta. Si bien la tarjeta que está clasificando actualmente es más pequeña que la anterior, la coloca en un lugar. Una vez que haya subido hasta la última carta y la haya colocado en su lugar, la mano se ordenará. Veamos cómo traduciríamos esta idea en ordenar una matriz de números enteros. Eche un vistazo al dibujo a continuación (la flecha marca el elemento que estamos ordenando actualmente y la llave marca la parte de la matriz con la que estamos trabajando actualmente):
Parece bastante simple, ¿eh? Entonces, ¿Cuál es la complejidad de este algoritmo?
Dado que necesitamos pasar por todos los elementos de nuestra matriz, y dado que es posible que también tengamos que intercambiarlos una vez por cada elemento anterior, este algoritmo resulta tener una complejidad de tiempo en el peor de los casos de O (n²), que no es realmente grandioso. Sin embargo, hay un lado positivo. Si sabemos que nuestra matriz estará casi ordenada cuando comencemos, este algoritmo se acercará al tiempo O (n), lo cual es realmente bueno. Esto significa que este algoritmo puede resultar muy útil cuando sabemos algo sobre los datos con los que estamos trabajando.
Otra gran característica de Insertion Sort es que se realiza en el lugar, lo que significa que no requerirá que asignemos más memoria para realizar la operación. Esto suele ser una muy buena hazaña, ya que las operaciones in situ suelen ser más rápidas que la asignación de nueva memoria. Digo generalmente, porque hay algunos algoritmos que pueden funcionar peor cuando intentas hacerlo de esta manera, Merge Sort es uno de ellos. En el caso de Insertion Sort, esta hazaña resulta ser una ventaja.
¿Cómo lo implementamos?
¡Me alegra que lo hayas preguntado! Dado que el ordenamiento por inserción es un algoritmo tan intuitivo, el código será bastante sencillo y fácil de entender. Mira esto:
array de extensión donde Elemento: Comparable {
public mutating func insertionSort () {
para iterationIndex en 0 .. <self.count {
var swapIndex =
iterationIndex while swapIndex> 0 {
if self [swapIndex] <self [swapIndex - 1] {
swapAt (swapIndex , swapIndex - 1)
swapIndex - = 1
} else {
break
}
} // finaliza mientras
} // finaliza para
} // finaliza la función
}
¿Qué estamos haciendo? Repasemos el código, paso a paso.
Primero, creamos un bucle for que hará un seguimiento del siguiente elemento que se ordenará. Luego usamos el iterationIndex variable para crear una variable de índice que podemos usar para intercambiar lentamente nuestro elemento por la matriz. Mientras swapIndex es mayor que 0 y el elemento en ese índice es menor que el anterior, seguimos intercambiando. Una vez que una de esas condiciones se vuelve falsa, rompemos y pasamos al siguiente elemento. ¡Simple como eso!
¡Eso es todo por esta vez! No dude en comentar si tiene preguntas y síganos para recibir notificaciones sobre artículos futuros.









Añadir comentario