Hola, me llamo Luis y aquí les traigo este nuevo tutorial.
Índice
Buscando otro algoritmo que involucra árboles binarios
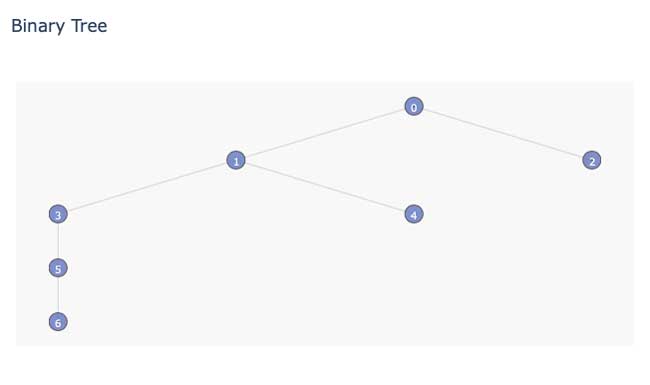
Entonces, dado un árbol binario como este:
¿Cuál es el diámetro del árbol?
Bueno, en realidad es bastante simple, es básicamente la distancia de par de nodos más larga del árbol .
Por ejemplo, la distancia entre el nodo 0 y 1 es solo 1. La distancia entre el nodo 4 y 0 es 2. Todo lo que tienes que hacer es imaginarte agarrando un nodo en cada una de tus manos y estirarlos en una línea recta, la longitud de la línea es la distancia entre los dos nodos.
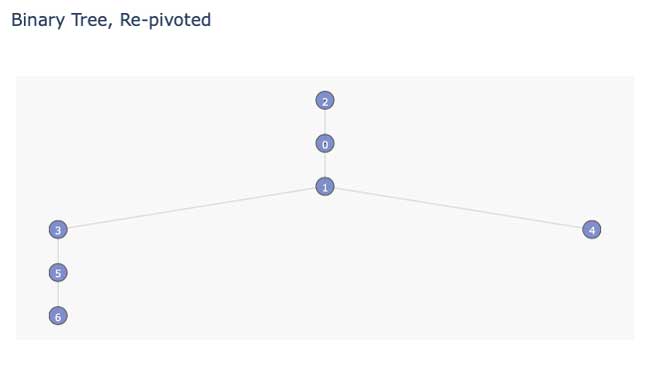
Entonces, ¿cuál es la distancia más larga, el diámetro, para este árbol entonces? Este árbol es lo suficientemente pequeño como para que puedas observarlo: es la distancia entre el nodo 2 y el nodo 6 y la distancia es 5:
La imagen de arriba es el árbol original, re-pivotado para que el nodo 2 sea la raíz, y puede ver que la distancia es claramente más larga de 2 a 6.
Entonces, ¿cómo hacemos para encontrar el diámetro?
Nuevamente, el primer sospechoso es una recursividad, primero atravesamos recursivamente el árbol, en cada nodo, encontramos el diámetro del hijo izquierdo y el hijo derecho, luego los sumamos para obtener el diámetro de la raíz.
¡Veamos si esto funciona! (no lo hace).
Este es mi arbol:
class Node: def __init__(self, value, left=None, right=None): self.value = value self.left = left self.right = right tree1 = Node(0) tree1.left = Node(1) tree1.right = Node(2) tree1.left.left = Node(3) tree1.left.right = Node(4) tree1.left.left.left = Node(5) tree1.left.left.left.left = Node(6)
Este es mi primer intento:
def find_diameter(tree): if tree is None: return None if tree.left is None and tree.right is None: return 0 left_diameter = find_diameter(tree.left) right_diameter = find_diameter(tree.right) diameter = (left_diameter + 1 if left_diameter is not None else 0) + \ (right_diameter + 1 if right_diameter is not None else 0) return diameter>>> print(find_diameter(tree1)) 6
Hmm, ¿no se supone que son 5?
Bueno, no es de extrañar, en el algoritmo, estamos encontrando el diámetro de los niños cada vez, así que en realidad estamos contando cada borde del árbol …
Esto no funcionará:
diameter = (left_diameter + 1 if left_diameter is not None else 0) + \ (right_diameter + 1 if right_diameter is not None else 0)
Porque está sumando los diámetros del niño izquierdo y el niño derecho. Lo que necesitamos es la longitud máxima del niño izquierdo y la longitud máxima del niño derecho, modifiquemos el algoritmo:
def find_diameter(tree): if tree is None: return None if tree.left is None and tree.right is None: return 0 left_length = find_diameter(tree.left) right_length = find_diameter(tree.right) diameter = max((left_length + 1 if left_length is not None else 0), (right_length + 1 if right_length is not None else 0)) return diameter
Hemos reemplazado «adición» con «max» , ¿funciona ahora?
>>> print(find_diameter(tree1)) 4
No, devolvió la longitud máxima de la raíz … pero lo que necesitamos es la longitud máxima del hijo izquierdo de la raíz más el hijo correcto de la raíz.
Podemos piratear esto llamando a find_diameter en el hijo izquierdo y el hijo derecho de la raíz y sumarlos, pero aún así no funcionará. ¿Por qué? ¡Porque el diámetro podría no pasar por la raíz!
Como ejemplo:
Claramente, el diámetro de este nuevo árbol va del nodo 6 al 5, 3, 1, 4, 7, 8, 9, 10, 11, y su longitud es 9.
!Variable de estado al rescate!
Lo que podemos hacer para resolver el problema es pasar una variable de estado «global_diameter» para realizar un seguimiento del diámetro más largo en cada nodo:
def find_diameter(tree, global_diameter): if tree is None: return None if tree.left is None and tree.right is None: return 0 # calculate maximum distance of left child and right child left_length = find_diameter(tree.left, global_diameter) right_length = find_diameter(tree.right, global_diameter) # calculate diameter of current node diameter = (left_length + 1 if left_length is not None else 0) + \ (right_length + 1 if right_length is not None else 0) # update global_diameter to the maximum local diameter global_diameter[0] = max(global_diameter[0], diameter) # calculate the max length of current node # so we can return it max_length = max((left_length + 1 if left_length is not None else 0), (right_length + 1 if right_length is not None else 0)) return max_length def entry_find_diameter(tree): global_diameter = [0] find_diameter(tree, global_diameter) return global_diameter[0]
En esta nueva versión, calculamos el diámetro en cada nodo y actualizamos global_diameter para que sea el máximo encontrado y devolvemos la longitud máxima en cada nodo para cada iteración (consulte la cadena más larga en un árbol binario para ver otra historia sobre este tema).
Probémoslo
>>> print(entry_find_diameter(tree1)) 5
¡Trabajos!
tree2 = Node(0) tree2.left = Node(1) tree2.right = Node(2) tree2.left.left = Node(3) tree2.left.right = Node(4, left=Node(7, left=Node(8, left=Node(9, left=Node(10, left=Node(11)))))) tree2.left.left.left = Node(5) tree2.left.left.left.left = Node(6) >>> print(entry_find_diameter(tree2)) 9
Funciona de nuevo.
Espero que te sea de utilidad, Gracias por leer este artículo.
Añadir comentario