Muy buenas, soy Luis y aquí les traigo este tutorial.
Desde el surgimiento de los campos del aprendizaje automático y la inteligencia artificial, la teoría de la probabilidad fue una herramienta poderosa que nos permitió manejar la incertidumbre en muchas aplicaciones, desde la clasificación hasta las tareas de pronóstico.
Hoy me gustaría hablarles más sobre el uso de Probabilidad y distribución Gaussiana en problemas de clustering, implementando en el camino el modelo GMM. Entonces empecemos.
Índice
¿Qué es GMM?
GMM (o modelos de mezcla gaussiana) es un algoritmo que utiliza la estimación de la densidad del conjunto de datos para dividir el conjunto de datos en un número preliminar definido de grupos.
Para una mejor comprensión, explicaré en paralelo la teoría y mostraré el código para implementarla.
La teoría y el código es la mejor combinación.
Primero, importemos todas las bibliotecas necesarias:
import numpy as np import pandas as pd
Recomiendo encarecidamente seguir los estándares de la biblioteca de aprendizaje de sci-kit al implementar un modelo por su cuenta.
Es por eso que implementaremos GMM como clase. Vamos también a la función __init_function.
class GMM:
def __init__(self, n_components, max_iter = 100, comp_names=None):
self.n_componets = n_components
self.max_iter = max_iter
if comp_names == None:
self.comp_names = [f"comp{index}" for index in range(self.n_componets)]
else:
self.comp_names = comp_names
# pi list contains the fraction of the dataset for every cluster
self.pi = [1/self.n_componets for comp in range(self.n_componets)]
Diciendo brevemente, n_componentes es el número de clúster en el que queremos dividir nuestros datos.
Max_iter representa el número de interacciones tomadas por el algoritmo y comp_names es una lista de cadenas con n_components número de elementos, que se interpretan como nombres de clústeres.
Entonces, antes de llegar al algoritmo EM, debemos dividir nuestro conjunto de datos. después de eso, debemos iniciar 2 listas.
Una lista que contiene los vectores medios (cada elemento del vector es la media de las columnas) para cada subconjunto. La segunda lista contiene la matriz de covarianza de cada subconjunto.
def fit(self, X):
# Spliting the data in n_componets sub-sets
new_X = np.array_split(X, self.n_componets)
# Initial computation of the mean-vector and covarience matrix
self.mean_vector = [np.mean(x, axis=0) for x in new_X]
self.covariance_matrixes = [np.cov(x.T) for x in new_X]
# Deleting the new_X matrix because we will not need it anymore
del new_X
Ahora podemos llegar al algoritmo EM.
Como su nombre lo indica, el algoritmo EM se divide en 2 pasos: E y M.
Durante el paso de Estimación, calculamos la matriz r. Se calcula utilizando la siguiente fórmula.
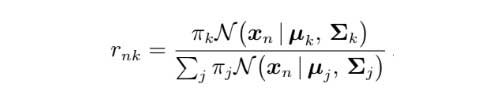
r (responsabilidades)r matriz también se conoce como 'responsabilidades' y se puede interpretar de la siguiente manera.
Las filas son las muestras del conjunto de datos, mientras que las columnas representan cada grupo, los elementos de esta matriz se interpretan de la siguiente manera: rnk es la probabilidad de que la muestra n forme parte del grupo k.
Cuando el algoritmo convergerá, usaremos esta matriz para predecir el grupo de puntos.
Además, calculamos la lista N, en la que cada elemento es básicamente la suma de la columna correspondiente en la matriz r. El siguiente código lo está haciendo.
for iteration in range(self.max_iter):
''' ---------------- E - STEP ------------------ '''
# Initiating the r matrix, evrey row contains the probabilities
# for every cluster for this row
self.r = np.zeros((len(X), self.n_componets))
# Calculating the r matrix
for n in range(len(X)):
for k in range(self.n_componets):
self.r[n][k] = self.pi[k] *
self.multivariate_normal(X[n], self.mean_vector[k],
self.covariance_matrixes[k])
self.r[n][k] /= sum([self.pi[j]*self.multivariate_normal(X[n], self.mean_vector[j],
self.covariance_matrixes[j]) for j in range(self.n_componets)])
# Calculating the N
N = np.sum(self.r, axis=0)
Señale que multivariate_normal es solo el formulario para la distribución normal aplicada a vectores, se usa para calcular la probabilidad de vectores en una distribución normal.
El código siguiente lo implementa, tomando el vector fila, el vector medio y la matriz de covarianza.
def multivariate_normal(self, X, mean_vector, covariance_matrix): return (2*np.pi)**(-len(X)/2)*np.linalg.det(covariance_matrix)**(-1/2)*np.exp(-np.dot(np.dot((X-mean_vector).T, np.linalg.inv(covariance_matrix)), (X-mean_vector))/2)
Parece un poco desordenado, pero puedes encontrar el código completo aquí.
Durante el paso de Maximización, estableceremos paso a paso el valor de los vectores medios y las matrices de covarianza para describir con ellos los grupos. Para hacer eso usaremos las siguientes fórmulas.
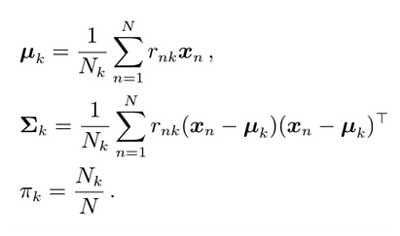
M-step.En el código me gustará eso:
''' --------------- M - STEP --------------- '''
# Initializing the mean vector as a zero vector
self.mean_vector = np.zeros((self.n_componets, len(X[0])))
# Updating the mean vector
for k in range(self.n_componets):
for n in range(len(X)):
self.mean_vector[k] += self.r[n][k] * X[n]
self.mean_vector = [1/N[k]*self.mean_vector[k] for k in range(self.n_componets)]
# Initiating the list of the covariance matrixes
self.covariance_matrixes = [np.zeros((len(X[0]), len(X[0]))) for k in range(self.n_componets)]
# Updating the covariance matrices
for k in range(self.n_componets):
self.covariance_matrixes[k] = np.cov(X.T, aweights=(self.r[:, k]), ddof=0)
self.covariance_matrixes = [1/N[k]*self.covariance_matrixes[k] for k in range(self.n_componets)]
# Updating the pi list
self.pi = [N[k]/len(X) for k in range(self.n_componets)]
Y hemos terminado con la función de ajuste. La aplicación etiológica del algoritmo EM hará que el GMM finalmente converja.
La función de predicción es realmente muy simple, simplemente usamos la función normal multivariante usando los vectores de media óptimos y las matrices de covarianza para cada grupo, para encontrar el uso que da los valores más grandes.
def predict(self, X):
probas = []
for n in range(len(X)):
probas.append([self.multivariate_normal(X[n],
self.mean_vector[k], self.covariance_matrixes[k])
for k in range(self.n_componets)])
cluster = []
for proba in probas:
cluster.append(self.comp_names[proba.index(max(proba))])
return cluster
Para probar el modelo, elegí compararlo con el GMM implementado en la biblioteca sci-kit. Generé 2 conjuntos de datos usando la función de generación de conjuntos de datos de aprendizaje de sci-kit: make_blobs con diferentes configuraciones. Entonces ese es el resultado.

sci-kit aprende uno.El agrupamiento de nuestro modelo y el de sci-kit es casi idéntico. Buen resultado. El código completo que puedes encontrar en este enlace.
- https://github.com/ScienceKot/mysklearn/tree/master/Gaussian%20Mixture%20Models
- https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm
- Matemáticas para el aprendizaje automático por Cheng Soon Ong, Marc Peter Deisenroth y A. Aldo Faisal.
Gracias por leer este tutorial.


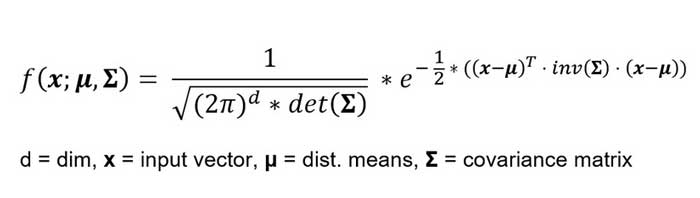






Añadir comentario