Estadísticas básicas para el análisis de datos con Python

Muy buenas, me llamo Miguel y aquí les traigo otro tutorial.

Cuando se trata de datos, a menudo necesitamos estar familiarizados con las estadísticas. Aquí, repasaremos algunos de los conceptos básicos absolutos de estadística, ¡se supone que debes saberlo!

Antes de comenzar, consideremos un conjunto de grupos de edad ordenados en orden ascendente, solo para hacer las cosas un poco más fáciles de entender, 10, 20, 30, 40, 50, 60, 70, 80, 90.

Promedio

En estadística, tenemos el media y el mediana y ambos se denominan promedios. Sin embargo, aparte de las estadísticas, la media se conoce comúnmente como promedio.

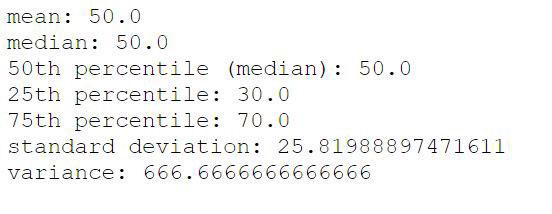
La media es el promedio más comúnmente conocido, y si toma nuestro conjunto de grupos de edad previamente definido, los suma todos y divide por el número total de valores, ¡el resultado obtenido no es más que la media de los grupos de edad! (10 + 20 + 30 + 40 + 50 + 60 + 70 + 80 + 90) / 10 = 45.

Del mismo modo, el mediana se refiere al valor medio de un conjunto de datos. En nuestro ejemplo, dado que hay 10 valores, el valor medio es el Quinto elemento, que es 50. Si hay un número par de puntos de datos, puede tomar la media de los dos valores en el medio para encontrar la mediana.

Percentiles

También puede visualizar la mediana como el percentil 50 o el 50% del conjunto de datos dado. Esto significa que el 50% de los datos es menor que la mediana y el 50% de los datos es mayor que la mediana. Esto nos dice dónde está la mitad de los datos, pero para obtener una comprensión más profunda de la distribución de datos, a menudo tendemos a mirar el percentil 25 y el percentil 75 del conjunto de datos dado.

los 25 El percentil es básicamente el 25% del conjunto de datos dado, que es una cuarta parte del conjunto total de datos. Del mismo modo, el 75º percentil es el 75% del conjunto de datos dado, que es tres cuartas partes del conjunto total de datos.

Si volvemos a mirar nuestras edades: 10, 20, 30, 40, 50, 60, 70, 80, 90,
Aquí, tenemos 9 valores, por lo tanto, el 25% de los datos serían aproximadamente 2 puntos de datos, por lo que el tercer punto de datos sería mayor que el 25% de los datos totales, lo que nos da el percentil 25 como 30 (el tercer punto de datos). .
De manera similar, el 75% de los datos son aproximadamente 6 puntos de datos, por lo tanto, el séptimo punto de datos es mayor que el 75% de los datos, por lo que el percentil 75 sería 70 (el séptimo punto de datos).

Podemos ver claramente que nuestros datos oscilan entre 10 y 90. Los percentiles 25 y 75 nos dicen que casi la mitad de nuestros grupos de edad se encuentran entre los 30 y los 70, lo que nos ayuda a comprender mejor cómo se distribuyen los datos.

Desviación estándar y varianza

Necesita desviación estándar y varianza si desea profundizar un poco más en la comprensión de la distribución de sus datos, básicamente nos ayuda a comprender cómo se distribuyen nuestros datos.

La desviación estándar es básicamente la raíz cuadrada de la varianza, así que primero, volvamos al ejemplo de nuestro grupo de edad: 10, 20, 30, 40, 50, 60, 70, 80, 90. Ahora, encontremos la media de los datos, que son 45. Entonces, se supone que debemos calcular qué tan lejos está cada valor en nuestro conjunto de datos, de la media. Por ejemplo, nuestro segundo elemento (20) está a 25 de la media (45-20 = 25). De manera similar, encuentre la distancia para todos y cada uno de los elementos del conjunto de datos.

Aquí hay una lista de todas estas distancias: 35, 25, 15, 5, 5, 15, 25, 35, 45 y luego cuadramos estos valores y los sumamos, lo que nos da 1225 + 625 + 225 + 25 + 25 + 225 + 625 + 1225 + 2025 = 6225. Ahora dividimos este valor por el número total de elementos en nuestro conjunto de datos y eso nos da la Varianza, 6225/9 = 666.66. Para obtener la desviación estándar, simplemente sacamos la raíz cuadrada de este número y obtenemos 25.81.

Dado que la media es 45 y la desviación estándar es 26,29, podemos decir que la mayoría de la población está entre 19,19 (45-25,81) y 70,81 (45 + 25,81), y así es como usamos la desviación estándar para tener una mejor idea de cómo los datos se distribuyen en nuestro conjunto de datos.

Estadísticas con Python

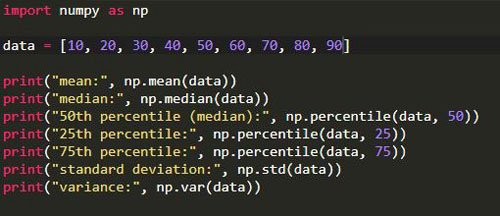
No creo en el hecho de que necesitas ser un genio de las estadísticas para convertirte en un científico de datos. No lo niego también… Si eres un genio en estadística siempre es mejor, ¡pero no es obligatorio! Si no está familiarizado con las estadísticas, ¡está bien! ¡Aún eres elegible para convertirte en un científico de datos! Simplemente revise algunas de las estadísticas básicas, aunque este artículo no cubre todos los conceptos básicos, aún puede comenzar con este artículo y continuar con mejores recursos. Una vez que esté seguro con la base, siempre puede usar Python u otros lenguajes de programación como R para hacer su trabajo. ¡Si! podemos calcular todas las operaciones que hemos discutido hasta ahora, con Python. Usaremos el paquete Python NumPy. Hay muchas más cosas útiles que puede hacer con NumPy, pero por ahora, solo usaremos algunas funciones para cálculos estadísticos: media, mediana, percentil, std, var.

Pruébalo:

importar numpy como np

datos = [11, 22, 33, 44, 55, 66, 77, 88, 99]

print ("mean:", np.mean (data))
print ("mediana:", np.median (datos))
print ("percentil 50 (mediana):", np.percentile (datos, 50))
print ("percentil 25:", np.percentile (datos, 25))
print ("percentil 75:", np.percentile (datos, 75))
print ("desviación estándar:", np.std (datos))
print ("varianza:", np.var (datos))

Y con eso, hemos cubierto los conceptos básicos absolutos de las estadísticas con Python. Definitivamente no es suficiente, así que asegúrese de explorar más.