Muy buenas, soy Luis y aquí les traigo otro nuevo artículo.
Support Vector Machine (SVM) es un método de clasificación que utiliza el concepto de hiperplano separador. Fue desarrollado en la década de 1990. Es una generalización de un clasificador intuitivo y simple llamado clasificador de margen máximo.
Para estudiar Support Vector Machine (SVM), primero debemos comprender qué es el clasificador de margen máximo y el clasificador de vectores de soporte.
En el clasificador de margen máximo, usamos un hiperplano para separar las clases. Pero, ¿Qué es un hiperplano? Considere que tenemos un espacio p-dimensional, un hiperplano es un subespacio afín plano (no necesariamente pasa del origen) de dimensión p-1. Por ejemplo, en un espacio bidimensional, un hiperplano es un subespacio plano unidimensional, que no es más que una línea. De manera similar, en un espacio tridimensional, un hiperplano es un subespacio plano bidimensional que no es más que un plano. La figura 1 ilustra un hiperplano en un espacio bidimensional.
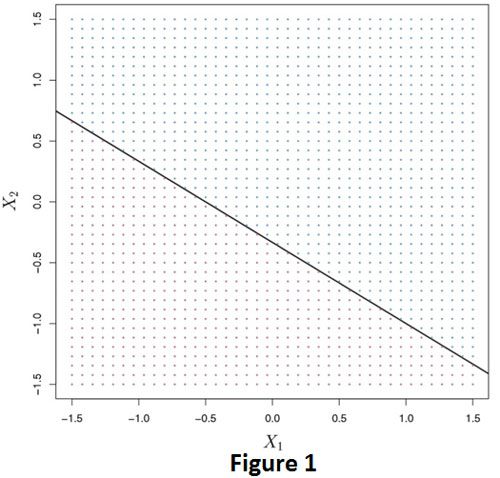
En la Figura 1, también podemos ver este hiperplano como una línea que divide el espacio en dos mitades. Por lo tanto, puede actuar como límite de decisión para la clasificación. Por ejemplo, en el panel de la derecha de la Figura 2, los puntos por encima de la línea pertenecen a la clase azul y los puntos por debajo de la línea pertenecen a la púrpura.

En general, si nuestros datos pueden separarse perfectamente usando un hiperplano, entonces existirá de hecho un número infinito de tales hiperplanos. Esto se debe a que un hiperplano de separación dado generalmente se puede desplazar un poquito hacia arriba o hacia abajo, o girar, sin entrar en contacto con ninguna de las observaciones. En el panel izquierdo de la Figura 2 se muestran tres posibles hiperplanos separadores. Para construir un clasificador basado en un hiperplano separador, debemos tener una forma razonable de decidir cuál de los infinitos hiperplanos separadores posibles usar. Una elección natural es la hiperplano de margen máximo (también conocido como el hiperplano de separación óptimo), que es el hiperplano de separación que está más alejado de las observaciones de entrenamiento. Es decir, podemos calcular la distancia (perpendicular) desde cada observación de entrenamiento a un hiperplano de separación dado; la distancia más pequeña es la distancia mínima desde las observaciones hasta el hiperplano, y se conoce como margen. El hiperplano de margen máximo es el hiperplano de separación para el que el margen es mayor – es decir, es el hiperplano que tiene la distancia mínima más lejana a las observaciones de entrenamiento. Luego, podemos clasificar una observación de prueba en función de qué lado del hiperplano de margen máximo se encuentra. Esto se conoce como clasificador de margen máximo. La Figura 3 muestra el hiperplano de margen máximo en los datos que se utilizan en la Figura 2.
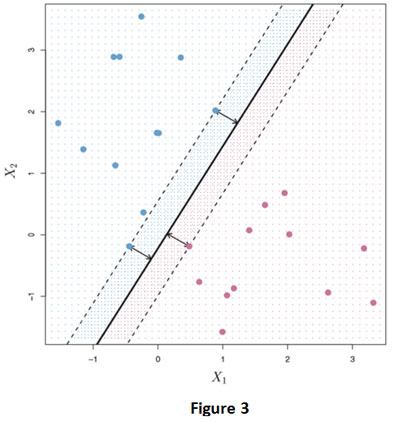
Comparando el panel de la derecha de la Figura 2 con la Figura 3, vemos que el hiperplano de margen máximo que se muestra en la Figura 3 de hecho resulta en una mayor distancia mínima entre las observaciones y el hiperplano de separación, es decir, un margen mayor. En un sentido, el hiperplano de margen máximo representa la línea media de la «losa» más ancha que podemos insertar entre las dos clases. Examinando la Figura 3, vemos que tres observaciones de entrenamiento son equidistantes del hiperplano del margen máximo y se encuentran a lo largo de las líneas discontinuas que indican el ancho del margen. Estas tres observaciones se conocen como vectores de soporte, ya que son vectores en el espacio p-dimensional (en la Figura 3, p = 2) y “apoyan” el hiperplano del margen máximo en el sentido de que si estos puntos se movieron ligeramente entonces el margen máximo el hiperplano también se movería. Curiosamente, el hiperplano de margen máximo depende directamente de los vectores de soporte, pero no de las otras observaciones: un movimiento a cualquiera de las otras observaciones no afectaría al hiperplano de separación, siempre que el movimiento de la observación no haga que cruce el límite establecido por el margen.
El hiperplano de margen máximo requiere la existencia de un hiperplano separador pero, en muchos casos, no existe un hiperplano separador. Es decir, no podemos separar exactamente las dos clases usando un hiperplano. Un ejemplo de esto se da en la Figura 4.

En este caso, no podemos separar exactamente las dos clases. Sin embargo, podemos extender el concepto de un hiperplano separador para desarrollar un hiperplano que casi separe las clases, usando un llamado margen suave. La generalización del clasificador de margen máximo al caso no separable se conoce como clasificador de vector de soporte.. En la Figura 4, vemos que las observaciones que pertenecen a dos clases no son necesariamente separables por un hiperplano. De hecho, incluso si existe un hiperplano separador, hay casos en los que un clasificador basado en un hiperplano separador podría no ser deseable. Un clasificador basado en un hiperplano separador clasificará necesariamente perfectamente todas las observaciones de entrenamiento; esto puede generar sensibilidad a las observaciones individuales. En la Figura 5 se muestra un ejemplo.
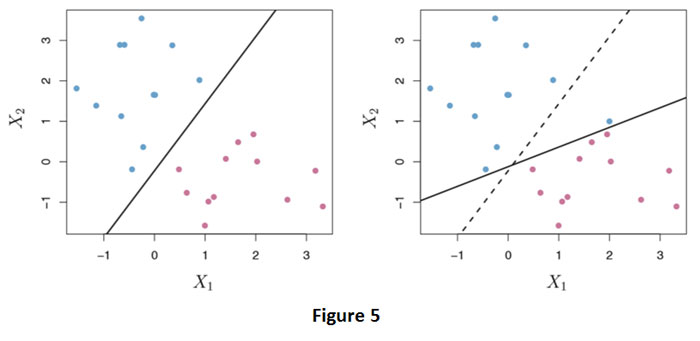
La adición de una única observación en el panel derecho de la Figura 5 conduce a un cambio dramático en el hiperplano del margen máximo. El hiperplano de margen máximo resultante no es satisfactorio; por un lado, tiene solo un margen pequeño. Esto es problemático porque, como se discutió anteriormente, la distancia de una observación desde el hiperplano puede verse como una medida de nuestra confianza en que la observación fue clasificada correctamente. Por lo tanto, podría valer la pena clasificar erróneamente algunas observaciones de entrenamiento para hacer un mejor trabajo en la clasificación de las observaciones restantes. El clasificador de vectores de soporte, a veces llamado clasificador de margen suave, hace exactamente esto. En lugar de buscar el margen más grande posible para que cada observación no solo esté en el lado correcto del hiperplano sino también en el lado correcto del margen, permitimos que algunas observaciones estén en el lado incorrecto del margen, o incluso en el lado incorrecto. lado del hiperplano. (El margen es suave porque puede ser violado por algunas de las observaciones de entrenamiento). Se muestra un ejemplo en el panel izquierdo de la Figura 6.
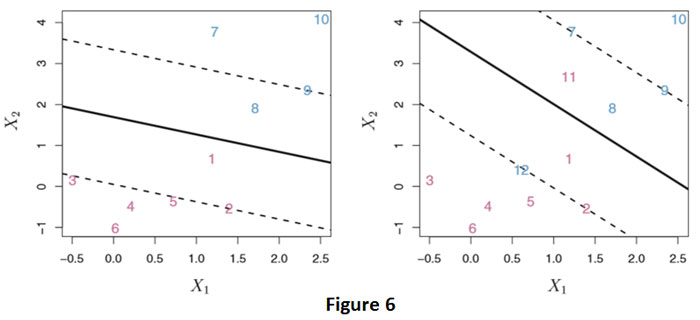
La mayoría de las observaciones están en el lado correcto del margen, pero un pequeño conjunto de observaciones está en el lado incorrecto del margen (observación 1 y 8). Una observación no solo puede estar en el lado incorrecto del margen, sino también en el lado incorrecto del hiperplano. En caso de que no exista ningún hiperplano, ese escenario es inevitable. Las observaciones que corresponden al lado incorrecto del hiperplano son observaciones que están mal clasificadas por el clasificador de vectores de soporte. Las observaciones que se encuentran en el lado correcto del margen no afectan el clasificador de vectores de soporte, pero las observaciones que se encuentran directamente en el margen, o en el lado incorrecto del margen para su clase, se conocen como vectores de soporte. Estas observaciones afectan al clasificador de vectores de soporte.
El clasificador de vectores de soporte es un enfoque natural para la clasificación en el entorno de dos clases, si el límite entre las dos clases es lineal. Sin embargo, en la práctica, a veces nos enfrentamos a límites de clase no lineales. Por ejemplo, considere los datos que se muestran en el panel izquierdo de la Figura 7.
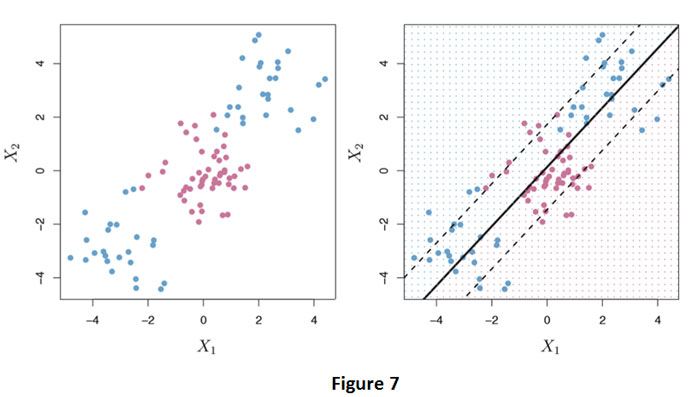
Está claro que un clasificador de vectores de soporte o cualquier clasificador lineal funcionará mal aquí. De hecho, el clasificador de vectores de soporte mostrado en el panel de la derecha de la Figura 7 es inútil aquí.
Podemos abordar este problema ampliando el espacio de características usando funciones polinomiales cuadráticas, cúbicas o de orden superior de las características. los máquina de vectores de soporte (SVM) es una extensión del clasificador de vectores de soporte que resulta de ampliar el espacio de características de una manera específica, usando kernels. Por ejemplo, en la Figura 7 tenemos dos características X1 y X2, en lugar de usar estas características como está para la clasificación, también podemos incluir términos de mayor grado de estas características. Por ejemplo, X1² y X2², lo que nos dará un polinomio cuadrático cuya solución no es lineal. Usamos granos para hacer exactamente esto de una manera eficiente, donde especificamos qué tipo de límite de decisión usar. Por ejemplo: lineal, polinomial (con algún grado) y radial. La Figura 8 ilustra el uso de kernel polinomial y radial en los datos de la Figura 7.
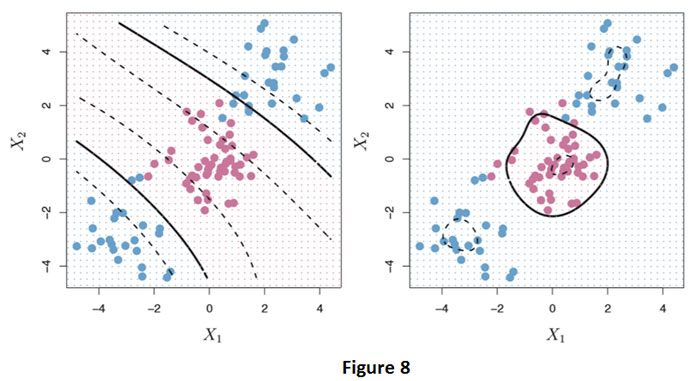
En el panel de la izquierda usamos un núcleo polinomial con grado 3 y en el de la derecha usamos un núcleo radial. Ambos núcleos dieron como resultado unas guías de decisión más apropiadas. Las matemáticas de cómo se obtienen los límites de decisión y los núcleos son demasiado técnicas para discutirlas aquí.
Referencia: Introducción al aprendizaje estadístico con aplicaciones en R, libro de Robert Tibshirani, Gareth James, Trevor Hastie y Daniela Witten.







Añadir comentario