Usando números de Fibonacci para abordar este algoritmo común
Un algoritmo común que se encuentra en las entrevistas técnicas es el problema de subir escaleras :
Estás subiendo una escalera. Se necesitan
npasos para llegar a la cima. Cada vez puedes subir1o2escalones. ¿De cuántas formas distintas puedes subir a la cima?
Por ejemplo, si la entrada fuera 2 (hay 2 escaleras en la escalera) , entonces hay 2 formas distintas de subir a la cima. Puede subir un escalón a la vez o subir ambos escalones a la vez.
Este es uno de esos problemas en los que hay muchas formas de resolverlo, incluida la recursividad, la memorización y la programación dinámica, pero la solución que más me gusta tiene que ver con el número de Fibonacci .
En esta publicación, explicaré cuáles son los números de Fibonacci, su relevancia para este problema y cómo resolver el algoritmo paso a paso.
Los números de Fibonnaci
Los números de Fibonacci (también conocidos como la secuencia de Fibonacci ) son una serie de números definidos por una ecuación recursiva:
Fn = Fn-1 + Fn-2
La secuencia comienza con F0 = 0 y F1 = 1.
Eso significa que F2 = 1, porque F2 = F1 + F0 = 1 + 0.
Luego, F3 = 2, porque F3 = F2 + F1 = 1 + 1.
La secuencia continúa infinitamente: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ... Puede leer más sobre los números de Fibonacci aquí.
Veamos a explicar algunos ejemplos del resultado esperado del problema de la escalera.
Podemos empezar con n = 0. Eso significa que la escalera tiene 0 escalones. Hay 0 formas de subir esta escalera, así que cuando n = 0, la salida = 0.

Cuando n = 1, la escalera tiene 1 escalón. Hay una forma de subir esta escalera, así que cuando n = 1, la salida = 1.

En el momento que n = 2, la escalera tiene 2 escalones. Ya que podemos subir 1 o 2 escaleras a la vez, hay 2 formas de subir esta escalera. Así que cuando n = 2, la salida = 2.

Cuando n = 3, la escalera tiene 3 escalones. Hay 3 formas de subir esta escalera.

Podemos seguir haciendo esto para cuando n = 4 (salida = 5)…

… Y n = 5 (salida = 8).

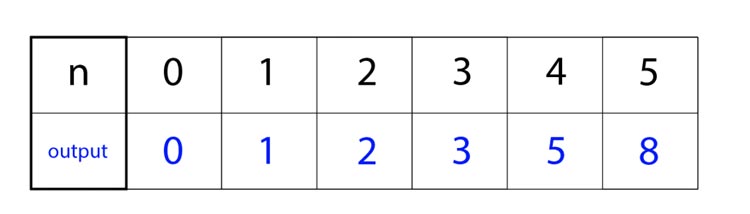
¡Podemos ver la secuencia de Fibonacci en nuestras salidas! Cada vez que incrementamos n, el número de formas de subir la escalera es la suma de las dos formas anteriores.
Eso significa que podemos resolver problemas de la escalera resolviendo el número de Fibonacci en cada escalera, hasta que lleguemos a n.
Resolviendo el algoritmo
Ahora que hemos reconocido el patrón en la salida, podemos seguir adelante y resolver el algoritmo. Para empezar, necesitamos escribir algunos casos base.
Cuando n es 0, 1 y 2, el número de formas de subir las escaleras 0, 1 y 2 (en ese orden), así que si n es uno de esos números, podemos devolver n.
function climbStairs(n) {
if (n < 3) return n;
//...
}
Necesitamos inicializar dos constantes, una llamada first y uno llamado second.
Empezaremos estableciendo first igual a 1, y second igual a 2.
Usaremos todos estos números para sumar el número actual en el que estamos y continuaremos cambiándolos.
function climbStairs(n) {
if (n < 3) return n;
let first = 1;
let second = 2;
//...
}
Ahora, comenzando en el número 2 y yendo hasta llegar a n, podemos tener un ciclo for incrementando un número a la vez.
Dentro del ciclo for, iniciaremos una nueva variable llamada current que almacenará la suma de first y second. Entonces, podemos movernos first más para igualar secondy seconda igual que current.
Una vez que termine el ciclo for, queremos devolver el número second que sea.
function climbStairs(n) {
if (n < 3) return n;
let first = 1;
let second = 2;
for (let i = 2; i < n; i++) {
const current = first + second;
first = second;
second = current;
}
return second;
}
¡Déjame saber en los comentarios si tienes alguna pregunta o idea sobre otras formas de resolver esto!
Gracias por leer este tutorial.








Añadir comentario