Hola, les saluda Miguel y en esta ocasión les traigo este post.
Dada una obra, ¿cómo identificamos a su autor? Este trabajo tuvo como objetivo dar una breve idea sobre la atribución de autoría utilizando Markov Chain.
La atribución de autoría (AA) es la tarea de identificar al autor de un texto determinado. No debe confundirse con los perfiles de autoría que se refieren a la información del autor, como la edad, el sexo o la etnia.
Comencemos con la suposición:
- AA asume que cada individuo tiene su propio estilo de escritura único y lo aplica constantemente a lo largo de su trabajo.
- Suponemos que el verdadero autor está en el grupo de candidatos a autor. Es decir: el modelo de predicción producirá una salida única del grupo de autores.
Índice
Características de estilometría
La idea principal detrás del AA es que al extraer algunas características textuales medibles (características de estilometría), podemos discriminar al verdadero autor del texto dado que comparte características similares.
Hay un r e muchos tipos de estilometría cuenta con una serie de características tales léxicas (palabras), las características de caracteres (frecuencia carta, n-gram etc), sintáctica cuenta (error, la frase estructura), las características semánticas (sinónimo, funcional) y funciones de aplicación específicos ( HTML, uso de saludo en correos electrónicos) (Stamatatos 2009).
Aquí, nos enfocamos en la característica de nivel de caracteres, tiene las ventajas de ser independiente del idioma (al menos para la mayoría de los idiomas) y resistente a los errores de ortografía (como el error tipográfico, en comparación con la característica léxica).
Cadena de Markov
La cadena de Markov es un proceso estocástico que modela la probabilidad del estado futuro únicamente por su estado actual. Fue introducido por el matemático ruso Andrey Markov.
El texto se puede ver como una secuencia de palabras o caracteres, donde la siguiente palabra o carácter se rige por el estilo estilométrico del autor.
Por lo tanto, se puede aplicar la cadena de Markov y las probabilidades de transición entre caracteres se pueden usar como una huella de autoría para distinguir entre autores.
Probabilidad logarítmica
La probabilidad de la secuencia de texto es el producto de todas las probabilidades de los personajes. Por ejemplo, tenemos las siguientes probabilidades:
P (H | T) = 0.02, es decir, la probabilidad del carácter H dada la corriente T es 0.02
P (E | H) = 0.03, es decir, la probabilidad del carácter E dada la corriente H es 0.03
La probabilidad del texto: THE es entonces 0.02 x 0.03 = 0.006
Por lo tanto, la probabilidad total de una secuencia larga de texto será extremadamente pequeña, lo que dificultará la comparación. En su lugar, se utiliza la probabilidad logarítmica.
La probabilidad del texto: THE es entonces log (0.02 x 0.03) = log (0.006) = -2.22
Implementación de Python
Usaremos algunos libros del Proyecto Gutenberg como nuestro conjunto de datos de entrenamiento y prueba.
Comenzamos importando el conjunto de datos de Gutenberg desde NLTK
import nltk
nltk.download('gutenberg')
nltk.corpus.gutenberg.fileids()

Hay 18 libros en el corpus NLTK Gutenberg, usamos ‘austen-sense.txt’ escrito por Jane Austen como los datos de prueba y comparar con ‘austen-emma.txt’ escrito por Jane Austen y ‘shakespeare-caesar.txt’ escrito por Shakespeare como datos de entrenamiento.
emma = nltk.corpus.gutenberg.words('austen-emma.txt')
emma = ' '.join(emma)caesar = nltk.corpus.gutenberg.words('shakespeare-caesar.txt')
caesar = ' '.join(caesar)sense = nltk.corpus.gutenberg.words('austen-sense.txt')
sense = ' '.join(sense)
Limitamos el número de estados en la cadena de Markov a 26 caracteres en inglés y espacio en blanco (“”).
state = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p","q", "r", "s", "t", "u", "v", "w", "x", "y", "z", " "]#create word2id and id2word dictionary char2id_dict = for index, char in enumerate(state): char2id_dict[char] = index
A continuación, definamos una función que cree una matriz de transición a partir de un texto dado.
import numpy as npdef create_transition_matrix(text): transition_matrix = np.zeros((27, 27)) for i in range(len(text)-1): current_char = text[i].lower() next_char = text[i+1].lower() if (current_char in state) & (next_char in state): current_char_id = char2id_dict[current_char] next_char_id = char2id_dict[next_char] transition_matrix[current_char_id][next_char_id] = transition_matrix[current_char_id][next_char_id] + 1sum_of_each_row_all = np.sum(transition_matrix, 1) for i in range (27): single_row_sum = sum_of_each_row_all[i] if (sum_of_each_row_all [i] == 0): single_row_sum = 1 transition_matrix[ i,: ] = transition_matrix[ i,: ] / single_row_sum return transition_matrix
Ahora, obtengamos la matriz de transición de los datos de entrenamiento.
TM_emma = create_transition_matrix(emma) TM_caesar = create_transition_matrix(caesar)
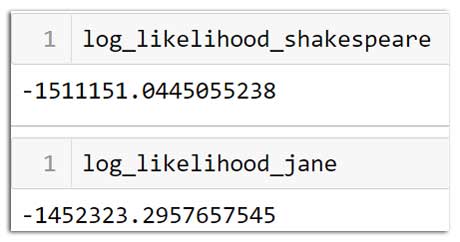
Comparamos la probabilidad logarítmica del libro ‘austen-sense.txt’ escrito por Jane Austen y Shakespeare.
log_likelihood_jane = 0 log_likelihood_shakespeare = 0for i in range(len(sense)-1): current_char = sense[i].lower() next_char = sense[i+1].lower()if (current_char in state) & (next_char in state): current_char_id = char2id_dict[current_char] next_char_id = char2id_dict[next_char] if TM_emma[current_char_id][next_char_id] != 0 and TM_caesar[current_char_id][next_char_id] != 0: log_likelihood_jane += np.log(TM_emma[current_char_id][next_char_id]) log_likelihood_shakespeare += np.log(TM_caesar[current_char_id][next_char_id])
Resultado
Por lo tanto, el texto dado tiene una mayor probabilidad de ser escrito por Jane Austen en comparación con Shakespeare. Asignamos la autoría del texto dado a Jane Austen. Para que esta demostración sea sencilla, solo usamos 1 libro desconocido y 2 autores. Puede aumentar el tamaño del conjunto de entrenamiento y prueba.
El código completo de la cadena de Markov de primer orden cargado en el github vinculado: https://github.com/yuanxy33/Authorship-Attribution.
Espero que te haya gustado el artículo. Gracias por leer.








Añadir comentario