He leído muchos tutoriales sobre el tema para averiguar cuál es mejor de dos y qué debo usar para mi modelo. No estaba satisfecho con ninguno de ellos y eso dejó a mi cerebro confundido, ¿Cuál debería usar?
Después de haber hecho tantos experimentos, finalmente encontré todas las respuestas a ¿Qué técnica de regularización utilizar y cuándo? Vayamos a ello usando un ejemplo de regresión.
Supongamos que tenemos un modelo de regresión para predecir valores del eje y basados en el valor del eje x.
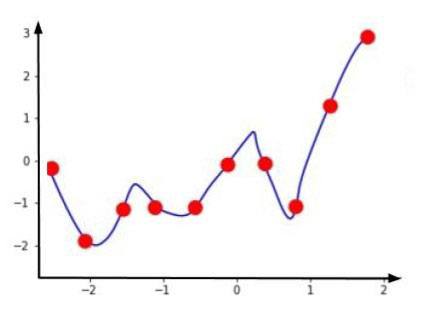

Mientras entrenamos el modelo, siempre tratamos de encontrar la función de coste. Aquí, y es la variable de salida real y ŷ es la salida prevista.
Entonces, para los datos de entrenamiento, nuestra función de coste será casi cero ya que nuestra línea de predicción pasa perfectamente desde los puntos de datos.
Ahora, supongamos que nuestro conjunto de datos nuevos de prueba tiene el siguiente aspecto
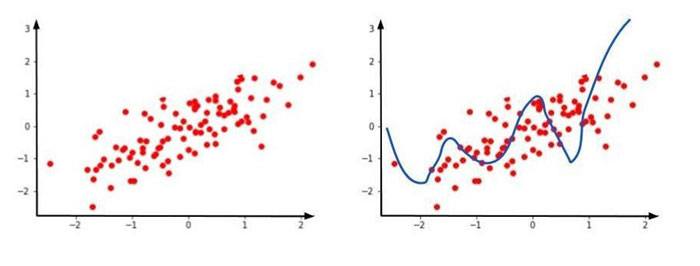
Aquí, claramente nuestra predicción está en otra parte y la línea de predicción se dirige a otra parte. Esto conduce a un sobreajuste.
El sobreajuste dice que con respecto al conjunto de datos de entrenamiento, está obteniendo un error bajo , pero con respecto al conjunto de datos nuevos de prueba, está obteniendo un error alto.
Recuerde, cuando necesitemos crear cualquier modelo, sea de regresión, clasificación, etc. Debería generalizarse.
Podemos usar la regularización L1 y L2 para hacer esta condición de sobreajuste que es básicamente de alta a baja variación.
Un modelo generalizado siempre debe tener un sesgo bajo y una varianza baja.
Tratemos de entender ahora cómo la regularización L1 y L2 ayudan a reducir esta condición.
Sabemos que la ecuación de una línea es y = mx + c.Para múltiples variables, esta línea se transformará en y = m1x1 + m2x2 + …… .. + mn xn.
Donde m1, m2,…., Mn son pendientes para las respectivas variables, y x1, x2, …., xn son las variables.
Cuando los coeficientes (es decir, pendientes) de las variables son grandes, cualquier modelo pasará a una condición de sobreajuste.
¿Por qué pasó esto? La razón es muy simple, cuanto mayor es el coeficiente, mayor es el peso de esa variable en particular en los modelos de predicción. Y sabemos que no todas las variables tienen una contribución significativa.
La regularización funciona penalizando a los grandes pesos. De esta forma, las variables altamente correlacionadas tienen pesos altos y las variables menos correlacionadas tienen un peso menor.
El método de regularización también es un hiperparámetro, lo que significa que puede ajustarse mediante validación cruzada.
Índice
Regresión de lasso o regularización L1
Un modelo de regresión que utiliza la técnica de regularización L1 se llama Regresión de lasso.
La regularización L1 funciona utilizando la función de error de la siguiente manera:

Para ajustar nuestros modelos siempre queremos reducir esta función de error. λ El parámetro nos dirá cuánto queremos penalizar los coeficientes.
Si λ es grande, penalizamos mucho. Si λ es pequeño, penalizamos menos. λ se selecciona mediante validación cruzada.
Anteriormente, nuestra función de error (o función de costo ∑ (y -ŷ) ² ) se basó únicamente en nuestra variable de predicción ŷ. Pero ahora tenemos λ (| m1 | + | m2 | +…. + | mn |) como término adicional.
Anteriormente la función de costo ∑ (y -ŷ) ²) = 0 ya que nuestra línea pasaba perfectamente por puntos de datos de entrenamiento.
sea λ = 1 y | m1 | + | m2 | +. . . . + | mn | = 2,8Función de error = ∑ (y -ŷ) ²) + λ (| m1 | + | m2 | +…. + | mn |) = 0 + 1 * 2.8 = 2.8
Mientras ajusta, nuestro modelo ahora intentará reducir este error de 2.8. digamos ahora el valor de ∑ (y -ŷ) ²) = 0.6, λ = 1 y | m1 | + | m2 | +. . . . + | mn | = 1,1
Ahora, el nuevo valor de la función Error será
Función de error = ∑ (y -ŷ) ²) + λ (| m1 | + | m2 | +…. + | mn |) = 0.6 + 1 * 1.1 = 1.7
Esto se repetirá varias veces. Para reducir la función de error, nuestras pendientes disminuirán simultáneamente. Aquí veremos que las pendientes se vuelven cada vez menos empinadas.
A medida que el valor de λ aumente, penalizará más los coeficientes y la pendiente de la línea irá más hacia cero.
En caso de regularización L1 por tomar | pendiente | en la fórmula, los pesos más pequeños eventualmente desaparecerán y se convertirán en 0.
Eso significa que la regularización L1 ayuda a seleccionar características que son importantes y convertir el resto en ceros.
Creará vectores dispersos de pesos como resultado como (0, 1, 1, 0, 1) . Por lo tanto, esto funciona bien para la selección de funciones en caso de que tengamos una gran cantidad de funciones.
Regularización L2 o regresión de crestas
Los modelos de regresión que utilizan la técnica de regularización L2 se llaman Regresión de crestas .
La regularización L2 funciona utilizando la siguiente función de error.
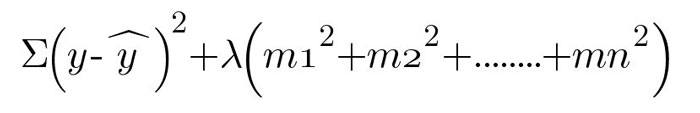
La regularización de L2 funciona de manera similar a como funciona L1 como se explicó anteriormente. La única diferencia entra en juego con las pistas.
En la regularización L1 estábamos tomando | pendiente | mientras aquí estamos tomando pendiente² .
Esto funcionará de manera similar, penalizará los coeficientes y la pendiente de la línea irá más hacia cero, pero nunca será igual a cero.
Esto se debe a que usamos pendiente² en la fórmula. Este método creará dispersión de pesos en forma de (0.5, 0.3, -0.2, 0.4, 0.1) . Entendamos esta escasez con un ejemplo.
Considerar los pesos (0, 1) y (0.5, 0.5)
Para los pesos (0, 1) L2: 0² + 1² = 1Para los pesos (0.5, 0.5) L2: 0.5² + 0.5² = 0.5
Por lo tanto, la regularización L2 preferirá el vector punto (0.5, 0.5) sobre el vector (1, 1) ya que esto produce una menor suma de cuadrados y a su vez, una función de error menor.
Gracias por leer este post.







Añadir comentario