Enseñar IA para aprender cómo los seres humanos planean de manera eficiente

Hola, les saluda Miguel y aquí les traigo un post.

Usando el aprendizaje de refuerzo para construir un modelo cognitivo de descubrimiento jerárquico

La planificación humana es jerárquica. Ya sea que planifiquemos algo simple como preparar la cena o algo complejo como un viaje al extranjero, normalmente empezamos con un bosquejo mental aproximado de las metas que queremos alcanzar («ir a la India, y luego regresar a casa»).

Este bosquejo se refina progresivamente en una secuencia detallada de subobjetivos («reservar el billete de avión», «empacar el equipaje»), subobjetivos, etc., hasta llegar a la secuencia real de movimientos corporales que es mucho más complicada que el plan original.

La planificación eficiente requiere el conocimiento de los conceptos abstractos de alto nivel que constituyen la esencia de los planes jerárquicos. Sin embargo, cómo los humanos aprenden tales abstracciones sigue siendo un misterio.

Aquí mostramos que los humanos forman espontáneamente tales conceptos de alto nivel de una manera que les permite planificar eficientemente dadas las tareas, recompensas y estructura de su entorno.

También mostramos que este comportamiento es consistente con un modelo formal de los cómputos subyacentes, fundamentando así estos hallazgos en principios computacionales establecidos y relacionándolos con estudios previos de planificación jerárquica.

La figura anterior muestra un ejemplo de planificación jerárquica, a saber, cómo alguien podría planear ir desde su oficina en Cambridge para comprar un vestido de novia de ensueño en Patna, India.

Los círculos representan estados y las flechas representan acciones de transición entre estados. Cada estado representa un grupo de estados en el nivel inferior. Las flechas más gruesas indican transiciones entre estados de nivel superior, que a menudo vienen a la mente primero.

Una perspectiva Bayesiana

Cuando se aplica a agentes inteligentes computacionalmente, la planificación jerárquica podría permitir modelos con capacidades de planificación avanzadas.

Las representaciones jerárquicas pueden ser modeladas desde un punto de vista bayesiano asumiendo un proceso generativo para la estructura de un entorno particular.

La labor actual sobre este problema incluye el desarrollo de un marco computacional para adquirir representaciones jerárquicas bajo un conjunto de supuestos simplificados sobre la jerarquía, es decir, modelando cómo las personas crean grupos de estados en sus representaciones mentales de entornos sin recompensa para facilitar la planificación.

En este trabajo, contribuimos con un modelo cognitivo bayesiano de descubrimiento jerárquico que combina el conocimiento de la agrupación y las recompensas para predecir la formación de agrupaciones, y comparamos el modelo con los datos obtenidos de los humanos.

Analizamos situaciones con mecanismos de recompensa tanto estáticos como dinámicos, encontrando que los humanos generalizan la información sobre las recompensas a los grupos de alto nivel y usan la información sobre las recompensas para crear grupos, y que la generalización de las recompensas y la formación de grupos basados en las recompensas puede ser predicha por nuestro modelo propuesto.

Antecedentes teóricos

Un área clave donde la psicología y la neurociencia se combinan es la comprensión formal del comportamiento humano en relación con las acciones asignadas. Nos preguntamos:

¿Cuál es la planificación y la metodología empleada por los agentes humanos cuando se enfrentan a la realización de alguna tarea? ¿Cómo descubren los humanos abstracciones útiles?

Esto es especialmente interesante a la luz de la capacidad única de los humanos y animales para adaptarse a nuevos entornos.

La literatura anterior sobre el aprendizaje animal sugiere que esta flexibilidad proviene de una representación jerárquica de objetivos que permite dividir las tareas complejas en subrutinas de bajo nivel que pueden extenderse a través de una variedad de contextos.

Chunking

El proceso de fragmentación se produce cuando las acciones se unen en secuencias de acción temporalmente extendidas que logran objetivos distantes.

El «chunking» suele ser el resultado de la transferencia del aprendizaje de un sistema dirigido a un objetivo a un sistema habitual, que ejecuta las acciones de forma estereotipada.

Desde un punto de vista computacional, esa representación jerárquica permite a los agentes ejecutar rápidamente acciones en un bucle abierto, reutilizar secuencias de acción conocidas cuando se encuentra un problema conocido, aprender más rápidamente ajustando las secuencias de acción establecidas para resolver problemas que recuerdan a los vistos anteriormente, y planificar en horizontes temporales ampliados.

Los agentes no necesitan preocuparse por las minúsculas tareas asociadas al logro de objetivos, por ejemplo, el objetivo de ir a la tienda se descompone en salir de la casa, caminar y entrar en la tienda en lugar de levantarse de la cama, mover el pie izquierdo hacia adelante, luego el derecho, etc.

Aprendizaje de refuerzo jerárquico

La cuestión de cómo los agentes deben tomar decisiones gratificantes es el tema del aprendizaje de refuerzo. El aprendizaje de refuerzo jerárquico (HRL) se ha convertido en el marco predominante para representar el aprendizaje y la planificación jerárquicos.

Dentro de la investigación sobre el modelado del HRL, se han presentado varias ideas sobre los posibles métodos de construcción de modelos. Nos centramos en la idea de que las personas organizan espontáneamente su entorno en grupos de estados que limitan la planificación.

Esta planificación jerárquica es más eficiente en tiempo y memoria que la planificación ingenua o plana, que incluye acciones de bajo nivel y es consistente con la limitada capacidad de memoria de trabajo de las personas [3].

En el diagrama que figura a continuación, los nodos y bordes gruesos indican que todos ellos deben ser considerados y mantenidos en la memoria a corto plazo para poder calcular el plan, y las flechas grises indican la pertenencia al grupo.

Observamos que la planificación de cómo pasar del estado s al estado g en el gráfico de bajo nivel G requiere al menos tantos pasos como los que realmente se ejecutan en el plan (arriba), la introducción del gráfico de alto nivel H alivia este problema reduce los costes de cálculo (medio), y la ampliación de la jerarquía recursiva reduce aún más el tiempo y la memoria necesarios para la planificación (abajo).

Las representaciones jerárquicas reducen los costos computacionales de la planificación [6]

Solway y otros proporcionan una definición formal de una jerarquía óptima, pero no especifican cómo podría descubrirla el cerebro [2].

Nuestra hipótesis es que una jerarquía óptima depende de la estructura del entorno, incluyendo tanto la estructura de los gráficos como la distribución de las características observables del entorno, específicamente las recompensas.

Modelo

Asumimos que los agentes representan su entorno como un gráfico, donde los nodos son estados del entorno y los bordes son transiciones entre estados. Los estados y transiciones pueden ser abstractos o tan concretos como las estaciones de metro y las líneas de tren que viajan entre ellas.

Estructura

Representamos el entorno observable como gráfico G = (V, E) y la jerarquía latente como H. Tanto G como H son gráficos no ponderados y no dirigidos. H consiste en cúmulos, donde cada nodo de bajo nivel en G pertenece exactamente a un cúmulo, y puentes, o bordes de alto nivel, que conectan estos cúmulos.

Los puentes pueden existir entre los cúmulos k y k’ sólo si hay un borde entre alguna v, v’ ∈ V tal que v ∈ k y v’∈ k’, es decir, cada borde de alto nivel en H tiene un correspondiente borde de bajo nivel en G.

En la ilustración que sigue, los colores denotan las asignaciones de los cúmulos. Los bordes negros se consideran durante la planificación, mientras que los bordes grises son ignorados por el planificador.

Los bordes gruesos corresponden a las transiciones entre los cúmulos. La transición entre los cúmulos w y z se realiza a través de un puente.

Ejemplo de gráfico de alto nivel (arriba) y gráfico de bajo nivel (abajo) [6]

Antes de la adición de las recompensas, el algoritmo de aprendizaje descubre las jerarquías óptimas dadas las siguientes restricciones:

• Pequeños grupos.
• Densa conectividad dentro de los grupos.
• La escasa conectividad entre los grupos.

Sin embargo, no queremos que los cúmulos sean demasiado pequeños – en el extremo, cada nodo es su propio cúmulo, lo que hace que la jerarquía sea inútil.

Además, aunque queremos una escasa conectividad entre los cúmulos, queremos mantener los puentes entre los cúmulos para preservar las propiedades de los gráficos subyacentes.

Utilizamos el Proceso de Restaurante Chino Estocástico de Tiempo Discreto (CRP) como prioritario para los clústeres.

El descubrimiento de las jerarquías se puede lograr invirtiendo el modelo generativo para obtener la probabilidad posterior de la jerarquía H. El modelo generativo presentado formalmente en [6] genera tales jerarquías.

Recompensas

En el contexto del gráfico G, las recompensas pueden interpretarse como características observables de los vértices. Dado que las personas a menudo se agrupan en función de características observables, es razonable modelar agrupaciones inducidas por las recompensas [5].

Además, suponemos que cada estado entrega una recompensa determinada al azar y que el objetivo del agente es maximizar la recompensa total [8].

Puesto que tenemos la hipótesis de que las agrupaciones inducen recompensas, modelamos cada agrupación como si tuviera una recompensa media.

Cada nodo de ese grupo tiene una recompensa media obtenida de una distribución centrada en la recompensa media del grupo. Por último, cada recompensa observada se extrae de una distribución centrada en la recompensa media de ese nodo. En [1] se ofrece un análisis formal.

Para simplificar la inferencia, primero asumimos que las recompensas son constantes, estáticas. Etiquetamos como dinámicas las recompensas que pueden cambiar entre observaciones con alguna probabilidad fija.

Realizamos dos experimentos para probar nuestra hipótesis sobre el comportamiento humano y comprender lo bien que podría ser predicho por nuestro modelo.

En particular, estudiamos hasta qué punto los cúmulos impulsan las inferencias sobre las recompensas, y hasta qué punto las recompensas impulsan la formación de cúmulos. Para cada experimento, recogimos datos humanos y los comparamos con las predicciones del modelo.

Los clústeres generan recompensas

El objetivo del primer experimento fue comprender cómo las recompensas se generalizan dentro de los grupos estatales. Probamos si la estructura del gráfico impulsa las formaciones de clústeres y si las personas generalizan una recompensa observada en un nodo al clúster al que pertenece el nodo.

Preparar

El experimento se llevó a cabo pidiendo a 32 sujetos humanos que eligieran un nodo para visitar a continuación, como se especifica en el siguiente escenario. A los participantes se les presentó al azar el gráfico a continuación o una versión invertida del mismo, para garantizar que no se introdujera un sesgo de lateralidad o estructura del gráfico.

Predijimos que los participantes elegirían el nodo adyacente al etiquetado que estaba ubicado en el grupo más grande, es decir, el nodo gris a la izquierda del azul en el primer caso, y el nodo gris a la derecha del azul en el primer caso. segundo caso.

A los participantes se les presentó la siguiente tarea y el gráfico asociado:

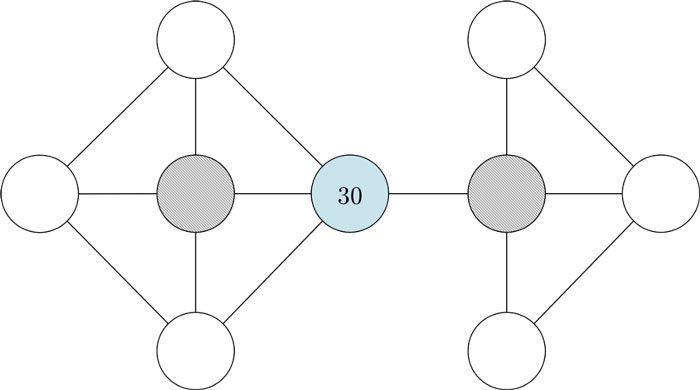
Trabaja en una gran mina de oro que se compone de múltiples minas y túneles individuales. El diseño de las minas se muestra en el diagrama a continuación (cada círculo representa una mina y cada línea representa un túnel).

Se le paga diariamente y se le paga $ 10 por gramo de oro que encontró ese día. Cavas exactamente una mina por día y registras la cantidad de oro (en gramos) que produjo la mina ese día.

Durante los últimos meses, ha descubierto que, en promedio, cada mina produce unos 15 gramos de oro al día. Ayer, excavó en la mina azul en el diagrama de abajo y obtuvo 30 gramos de oro. ¿En cuál de las dos minas sombreadas excavarás hoy? Encierre en un círculo la mina que elija.

Gráfico de minas presentado a los participantes [1]

Esperábamos que la mayoría de los participantes identificaran automáticamente los siguientes grupos, con nodos coloreados en melocotón y lavanda para denotar los diferentes grupos, y tomaran una decisión sobre cuál mina seleccionar teniendo en cuenta estos grupos.

Se planteó la hipótesis de que los participantes seleccionarían un nodo de color melocotón en lugar de uno lavanda, ya que el nodo con la etiqueta 30, una recompensa bastante mayor que la media, está en el grupo de color melocotón.

Gráfico de minas presentado a los participantes, con probables grupos mostrados [1]

Inferencia

Aproximamos la inferencia bayesiana sobre H utilizando un muestreo de Metrópolis dentro de Gibbs [4], que actualiza cada componente de H tomando muestras de su posterior, condicionando todos los demás componentes en un solo paso de Metropolis-Hastings.

Empleamos un paseo aleatorio gaussiano como la distribución de la propuesta para los componentes continuos y el CRP condicional antes como la distribución de la propuesta para las asignaciones de conglomerados. [7].

El enfoque puede interpretarse como una escalada estocástica con respecto a una función de utilidad definida por el posterior.

Resultados

Hubo 32 participantes en cada uno de los grupos humanos y simulados. Los tres grupos principales generados por el modelo se muestran a continuación (panel izquierdo).

Los tres resultados principales fueron los mismos, lo que indica que el modelo identificó las agrupaciones de colores con alta confianza.

Los resultados de los participantes, así como los del modelo de recompensas estático, se visualizan en el gráfico de barras a continuación (panel derecho), que muestra la proporción de sujetos humanos y simulados que eligieron visitar el nodo 2 a continuación. La línea negra continua indica la media y las líneas negras punteadas indican los percentiles 2.5 y 97.5.

Resultados del experimento de generalización de recompensas dentro de grupos [1]

Los valores p enumerados en la siguiente tabla se calcularon mediante una prueba binomial de cola derecha, donde se asumió que el nulo era una distribución binomial sobre la elección del nodo gris izquierdo o derecho.

Se consideró que el nivel de significancia era 0.05, y tanto los resultados experimentales humanos como los resultados del modelado fueron estadísticamente significativos.

Acciones realizadas por humanos y modelo de recompensas estático [1]

Las recompensas inducen agrupaciones

En el segundo experimento, el objetivo era determinar si las recompensas inducen agrupaciones. Predijimos que los nodos con la misma recompensa colocados adyacentes entre sí se agruparían, incluso si la estructura del gráfico por sí sola no induciría grupos.

Recuerde que Solway et. al demostró que las personas prefieren caminos que cruzan la menor cantidad de límites jerárquicos [2]. Por lo tanto, entre dos caminos idénticos, la única razón para preferir uno sobre el otro sería porque cruza menos límites jerárquicos.

Un posible contraargumento a esto es que la gente elige el camino con mayores recompensas. Sin embargo, en nuestra configuración que se detalla a continuación, las recompensas se otorgan solo en el estado objetivo, no de forma acumulativa a lo largo del camino tomado.

Además, la magnitud de las recompensas varió entre las pruebas. Por lo tanto, es poco probable que las personas favorezcan un camino porque los nodos a lo largo de ese camino tienen recompensas más altas.

Preparar

Este experimento se realizó en la web utilizando Amazon Mechanical Turk (MTurk). Los participantes recibieron el siguiente contexto sobre la tarea:

Imagina que eres un minero que trabaja en una red de minas de oro conectadas por túneles. Cada mina produce una cierta cantidad de oro (puntos) cada día. Cada día, su trabajo es navegar desde una mina inicial a una mina objetivo y recolectar los puntos de la mina objetivo.

Algunos días, podrá elegir la mina que desee. En esos días, debe intentar elegir la mina que rinda más puntos. El resto de días, solo habrá una mina disponible. Los puntos de esa mina se escribirán en verde y las otras minas aparecerán en gris.

En esos días, debes navegar hasta la mina disponible. Los puntos de cada mina estarán escritos en él. La mina actual se resaltará con un borde grueso. Puede navegar entre las minas usando las teclas de flecha (arriba, abajo, izquierda, derecha).

Una vez que llegue a la mina objetivo, presione la tecla espaciadora para recolectar los puntos y comenzar el día siguiente. Habrá 100 días (pruebas) en el experimento.

Se presentó a los participantes el siguiente gráfico (panel izquierdo). Como en el experimento anterior, a los participantes se les dio aleatoriamente la configuración mostrada o la versión invertida horizontalmente del mismo gráfico para controlar la posible asimetría de izquierda a derecha. También se muestran los grupos inducidos esperados, con los nodos numerados como referencia (panel derecho).

Gráfico de minas presentado a los participantes de MTurk (izquierda), con probables grupos mostrados (derecha) [1]

Nos referiremos al primer caso, donde los participantes son libres de navegar a cualquier mina, como libre elección y el segundo caso, donde los participantes navegan a una mina específica, como elección fija. Los participantes recibieron una recompensa monetaria por cada ensayo para desalentar las respuestas aleatorias.

En cada prueba, los valores de recompensa se cambiaron con una probabilidad de 0,2. Las nuevas recompensas se extrajeron uniformemente al azar del intervalo [0, 300].

Sin embargo, la agrupación de recompensas siguió siendo la misma en todas las pruebas: los nodos 1, 2 y 3 siempre tenían un valor de recompensa, los nodos 4, 5 y 6 tenían un valor de recompensa diferente y los nodos 7, 8, 9 y 10 tenían un valor de recompensa diferente. tercer valor de recompensa.

Los primeros 99 ensayos permitieron al participante desarrollar una jerarquía de grupos. La prueba final, que actuó como prueba de prueba, pidió a los participantes que navegaran del nodo 6 al nodo 1.

Suponiendo que las recompensas indujeron los grupos que se muestran arriba, predijimos que más participantes tomarían el camino a través del nodo 5, que cruza solo un grupo límite, sobre el uno al nodo 7, que cruza dos límites de clúster.

Inferencia

Modelamos el caso de opción fija, asumiendo que las tareas en los 100 ensayos eran todas iguales a las del ensayo número 100 presentado a los participantes, el ensayo de prueba.

Primero, asumimos recompensas estáticas, donde las recompensas permanecieron constantes en todas las pruebas. A continuación, asumimos recompensas dinámicas, donde las recompensas cambiaban para cada prueba.

En contraste con el experimento anterior, donde el participante elige un solo nodo, el modelo predice ese nodo, este experimento se ocupa del segundo nodo de la ruta completa que el participante eligió tomar desde el nodo inicial hasta el nodo objetivo.

Por lo tanto, para comparar el modelo con los datos humanos, utilizamos una variante de búsqueda en amplitud, en lo sucesivo denominada BFS jerárquica, para predecir una ruta desde el nodo de inicio (nodo 6) hasta el objetivo (nodo 1).

Recompensas estáticas

Para cada sujeto, tomamos una muestra de la parte posterior utilizando el muestreo de Metrópolis dentro de Gibbs y elegimos la jerarquía más probable, es decir, la jerarquía con la probabilidad posterior más alta. Luego, usamos BFS jerárquico para encontrar primero una ruta entre los clústeres y luego entre los nodos dentro de los clústeres.

Recompensas dinámicas

Para las recompensas dinámicas, usamos la inferencia en línea. Para cada participante simulado, permitimos que el muestreo de cada ensayo progresara solo en 10 pasos. Luego, guardamos la jerarquía y agregamos información sobre las recompensas modificadas.

A continuación, permitimos que el muestreo progresara nuevamente, comenzando desde la jerarquía guardada. Al igual que en el experimento humano, al comienzo de cada prueba, había una probabilidad de 0,2 de que las recompensas se volvieran a asignar al azar a nuevos valores, aunque las recompensas siempre eran iguales dentro de los grupos.

Este método de inferencia simuló cómo los participantes humanos podrían aprender acumulativamente en el transcurso de muchos ensayos. Asumimos, para el propósito de este experimento, que las personas solo tienen en mente una jerarquía a la vez, en lugar de actualizar múltiples jerarquías en paralelo.

También modificamos el registro posterior para penalizar los clústeres desconectados, porque dichos clústeres se volvieron mucho más comunes bajo este tipo de inferencia.

Resultados

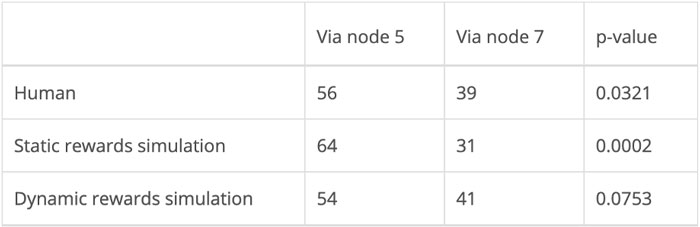
Hubo 95 participantes en cada uno de los grupos humanos y dos simulados. La hipótesis nula está representada por un número igual de participantes que eligen una ruta a través del nodo 5 y a través del nodo 7, ya que en ausencia de cualquier otra información y dado que ambas rutas tienen la misma longitud, es igualmente probable que un participante elija una de las dos.

Acciones realizadas por humanos y modelos de recompensas estáticos y dinámicos [1]

Como se indica en la tabla anterior, los resultados del experimento humano y el modelado de recompensas estáticas fueron estadísticamente significativos en α = 0.05.

Además, como se muestra a continuación, los resultados del experimento humano están en el percentil 90 de una distribución normal centrada alrededor de 0,5, la proporción esperada dada la hipótesis nula.

En la figura, incluimos agrupaciones identificadas por el modelo de recompensas estáticas (primera fila), el modelo de recompensas estáticas con formación de agrupaciones entre componentes desconectados penalizados en la segunda fila) y el modelo de recompensas dinámicas (tercera fila).

Clústeres identificados por simulaciones [1]

Recompensas estáticas

Usamos 1000 iteraciones de muestreo de Metropolis dentro de Gibbs para generar cada muestra, con un burnin y un retraso de 1 cada uno.

La simulación bajo recompensas estáticas ciertamente favorece las rutas a través del nodo 5, a un nivel que es estadísticamente significativo.

Además, dado que su propósito es modelar el comportamiento humano, este resultado es significativo a la luz de que los datos humanos también son estadísticamente significativos (0.0321 <α = 0.05).

Elecciones de sujetos humanos y simulados [1]

Recompensas dinámicas. Para imitar los ensayos en humanos, realizamos 100 ensayos, cada uno con 10 iteraciones de Metropolis-within-Gibbs para tomar muestras de la parte posterior.

El burnin y lag se establecieron nuevamente en 1. El método de inferencia en línea parece haber modelado los datos humanos mejor que el modelado de recompensas estáticas.

Aunque el grupo de participantes simulados bajo el modelado de recompensas dinámicas está más lejos de la hipótesis que el grupo simulado bajo recompensas estáticas modelado.

56 participantes humanos y 54 participantes simulados bajo el modelo de recompensas dinámicas eligieron pasar por el nodo 5 (una diferencia del 3,4%), en comparación con 64 participantes simulados bajo el modelo de recompensas estáticas (una diferencia del 18,5%).

El gráfico de barras de arriba visualiza la proporción de sujetos humanos y simulados cuyo segundo nodo de ruta elegido fue el nodo 5. La línea negra continua indica la proporción esperada dada la hipótesis nula y las líneas negras punteadas indican los percentiles 10 y 90.

Conclusiones

Los seres humanos parecen organizar espontáneamente los entornos en grupos de estados que apoyan la planificación jerárquica, lo que les permite abordar los problemas más difíciles descomponiéndolos en subproblemas a varios niveles de abstracción. La gente confía constantemente en estas presentaciones jerárquicas para llevar a cabo tareas grandes y pequeñas – desde planificar el día, hasta organizar una boda, o conseguir un doctorado – a menudo con éxito en el primer intento.

Hemos demostrado que una jerarquía óptima depende no sólo de la estructura de los gráficos, sino también de las características observables del entorno, es decir, de la distribución de las recompensas.

Construimos modelos bayesianos jerárquicos para comprender cómo los cúmulos inducen recompensas estáticas y cómo las recompensas estáticas y dinámicas inducen cúmulos, y encontramos que la mayoría de los resultados eran estadísticamente significativos en términos de cuán cerca nuestros modelos capturaban las acciones humanas.

Todos los archivos de datos y código de todas las simulaciones y experimentos presentados están disponibles en el repositorio de GitHub enlazado aquí. Esperamos que el modelo presentado, así como los resultados relacionados en un documento reciente, allanen el camino para futuros estudios para investigar los algoritmos neurales que apoyan la capacidad cognitiva esencial de la planificación jerárquica.

Referencias

[1] A. Kumar y S. Yagati, Generalización de recompensas y descubrimiento de jerarquía basada en recompensas para la planificación (2018), MIT

[2] A. Solway, C. Diuk, N. Córdova, D. Yee, A. Barto, Y. Niv y M. Botvinick, Jerarquía conductual óptima (2014), PLOS Computational Biology

[3] G. Miller, El número mágico siete más o menos dos: Algunos límites en nuestra capacidad para procesar información (1956), The Psychological Review

[4] G. Roberts y J. Rosenthal, Examples of Adaptive MCMC (2009), Journal of Computational and Graphical Statistics

[5] J. Balaguer, H. Spiers, D. Hassabis y C. Summerfield, Mecanismos neuronales de planificación jerárquica en una red de metro virtual (2016), Neuron

[6] M. Tomov, S. Yagati, A. Kumar, W. Yang y S. Gershman, Descubrimiento de representaciones jerárquicas para una planificación eficiente (2020), PLOS Computational Biology

[7] R. Neal, Métodos de muestreo en cadena de Markov para modelos de mezcla de procesos de Dirichlet (2000), Journal of Computational and Graphical Statistics

[8] R. Sutton y A. Barto, Aprendizaje por refuerzo: una introducción (2018), The MIT Press.

Gracias por leer hasta el final.

---