Comprensión del teorema del límite central

Hola, me llamo Miguel y para hoy les traigo un artículo.

Antes de codificar, una revisión rápida

Hoy quiero analizar el teorema del límite central y cómo se relaciona con gran parte del trabajo que realiza un científico de datos.

Actualización de histograma

Lo primero es lo primero, una herramienta fundamental para cualquier científico de datos es un tipo de gráfico muy simple llamado histograma. Si bien seguramente ha visto muchos histogramas, a menudo pasamos por alto su significado. El propósito principal de un histograma es comprender la distribución de un conjunto de datos determinado.

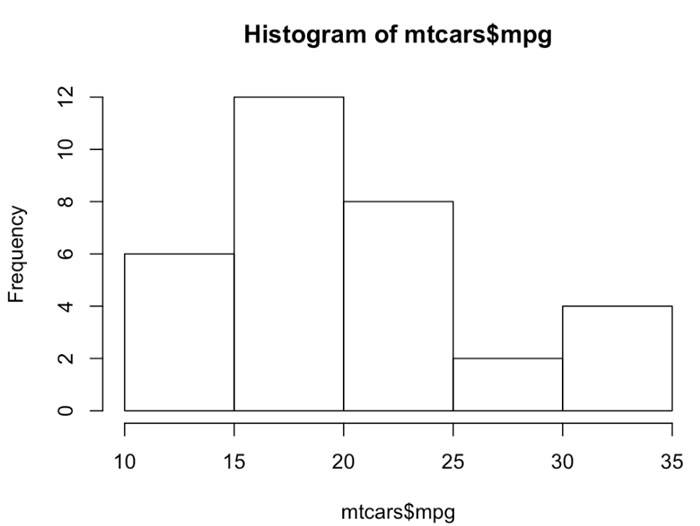
Como recordatorio, un histograma representa el número de ocurrencias en el eje y de diferentes valores de una variable, que se encuentran en el eje x.

Aquí hay un ejemplo de esto, queremos comprender la distribución de millas por galón en la población de automóviles en nuestro conjunto de datos. Aquí estamos usando el mtcars conjunto de datos y puedo ver que en el lado derecho de nuestro gráfico hay un poco de cola; este histograma es lo que se conoce como sesgado a la derecha. El concepto detrás de esto es que sí, hay autos en el extremo del millaje de gasolina, pero son muy pocos.

Distribuciones normales estándar

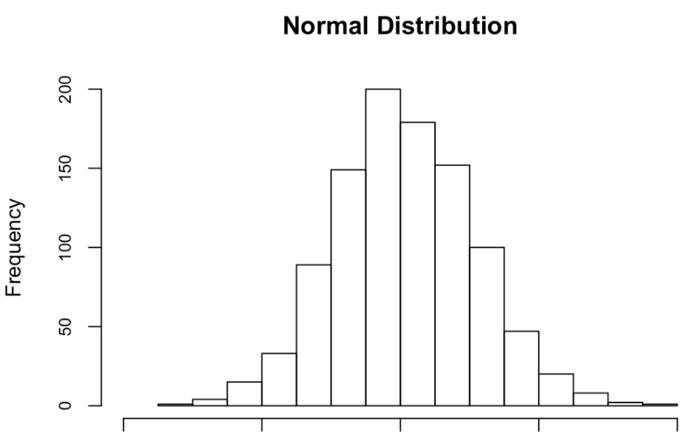
Similar a lo que acaba de ver, la distribución clásica que probablemente haya visto es lo que se conoce como distribución normal, también conocida como curva de campana o distribución normal estándar. La idea central es que la «distribución» de ocurrencias es simétrica .

Eche un vistazo a la trama a continuación. Vemos un histograma similar al anterior, más bien aquí es mucho más simétrico.

¿Qué es exactamente el teorema del límite central?

El teorema del límite central establece que la distribución de las medias muestrales debe ser aproximadamente normal.

Veamos el teorema en práctica

Considere el siguiente ejemplo. Supongamos que trabaja en una universidad y quiere comprender la distribución de los ingresos en el primer año fuera de la escuela de un alumno.

El hecho es que no podrá recopilar ese punto de datos para cada alumno. Alternativamente, muestreará la población varias veces obteniendo medias de muestra individuales para cada «muestra».

Ahora graficamos las medias de la muestra mediante un histograma y podemos ver el surgimiento de una distribución normal.

La conclusión clave aquí es que incluso si las variables de entrada no están distribuidas normalmente, la distribución muestral se aproximará a la distribución normal estándar.

¡Codifiquemos!

Como demostración final de esta idea, inicialmente trazamos la distribución de MPG de la mtcars conjunto de datos. Aquí dividimos un vector para cada una de las muestras de mpg, luego recorrimos 50 muestras, cada una tomando la media de diez registros aleatorios en el conjunto de datos. Una vez más, los trazamos como un histograma y podemos ver que surge una distribución normal.

mpg_samples <- c()for (i in 1:50)  
mpg_samples[i] = mean(sample(mtcars$mpg, 10, replace = TRUE))
 
hist(mpg_samples, col = 'purple', xlab = "MPG")

Esto debería servir como un concepto fundamental para su capacitación en ciencia de datos, que es fundamental para la prueba de hipótesis, la experimentación, entre otros métodos y técnicas de ciencia de datos.

¡Espero que hayas encontrado esto útil!

Feliz ciencia de datos.