Bienvenido, soy Miguel y aquí les traigo este nuevo post.
Índice
Visión general
Uno de los problemas espaciales más comunes es encontrar el punto de interés (PDI) más cercano a nuestra ubicación actual.
Digamos que alguien se quedará sin gasolina pronto y necesita encontrar la gasolinera más cercana antes de que sea demasiado tarde, ¿cuál es la mejor solución para este problema?
Seguro que el conductor puede consultar el mapa para encontrar la estación de servicio más cercana, pero puede ser problemático si hay más de una estación en el área y necesita decidir rápidamente cuál es la más cercana.
La mejor solución es representar cada PDI con un punto dentro de una forma poligonal. Entonces, dentro de un polígono, el PDI más cercano es definitivamente el punto dentro del polígono. Estos polígonos se denominan regiones de Voronoi.
Recopilación de datos
Para este proyecto, creo regiones de Voronoi en el mapa en función de los datos de PDI. Todos los datos de PDI se eligen aleatoriamente mientras que los datos de la red de calles se descargan de OpenStreetMap con la ayuda del paquete OSMnx.
Crear regiones de Voronoi
Actualmente, la forma más fácil de construir regiones de Voronoi usando Python es usando el paquete geovoronoi.
Geovoronoi es un paquete para crear y trazar regiones de Voronoi dentro de áreas geográficas. En cuanto a la visualización del mapa, elijo el paquete folium.
Primero empiezo creando puntos aleatorios alrededor del mapa.
gdf = gpd.GeoDataFrame()
gdf = gdf.append('geometry': Point(106.644085,-6.305286), ignore_index=True)
gdf = gdf.append('geometry': Point(106.653261,-6.301309), ignore_index=True)
gdf = gdf.append('geometry': Point(106.637751,-6.284774), ignore_index=True)
gdf = gdf.append('geometry': Point(106.665062,-6.284598), ignore_index=True)
gdf = gdf.append('geometry': Point(106.627582,-6.283521), ignore_index=True)
gdf = gdf.append('geometry': Point(106.641365,-6.276593), ignore_index=True)
gdf = gdf.append('geometry': Point(106.625972,-6.303643), ignore_index=True)
El siguiente paso es determinar el área de cobertura de las regiones de Voronoi y guardarlo en el geodataframe.
area_max_lon = 106.670929
area_min_lon = 106.619602
area_max_lat = -6.275227
area_min_lat = -6.309795
lat_point_list = [area_min_lat, area_max_lat,area_max_lat,area_min_lat]
lon_point_list = [area_min_lon, area_min_lon, area_max_lon, area_max_lon]
polygon_geom = Polygon(zip(lon_point_list, lat_point_list))
boundary = gpd.GeoDataFrame()
boundary = boundary.append('geometry': polygon_geom, ignore_index=True)
No olvide convertir los marcos de datos gdf y de límites a la proyección de Web Mercator.
gdf.crs = 'init' :'epsg:3395' boundary.crs = 'init' :'epsg:3395'
Convierta el marco de datos de geometría de límites en una unión del polígono y el marco de datos de puntos de interés en una matriz de coordenadas.
boundary_shape = cascaded_union(boundary.geometry) coords = points_to_coords(gdf.geometry)
Calcula las regiones de Voronoi.
poly_shapes, pts, poly_to_pt_assignments = voronoi_regions_from_coords(coords, boundary_shape)
Cree un gráfico de OpenStreetMap dentro de los límites del área de cobertura. Usar el gráfico para recopilar todas las redes de calles dentro de los límites del área de cobertura y guardarlo en un marco de datos.
G = ox.graph_from_polygon(boundary_shape, network_type='all_private') gdf_all_streets = ox.graph_to_gdfs(G, nodes=False, edges=True,node_geometry=False, fill_edge_geometry=True)
Cree un nuevo marco de datos para recopilar redes de calles dentro de cada región de Voronoi
gdf_streets_by_region = gpd.GeoDataFrame() for x in range(len(poly_shapes)): gdf_streets = gpd.GeoDataFrame() gdf_streets['geometry'] = gdf_all_streets.intersection(poly_shapes[x]) gdf_streets['voronoi_region'] = x gdf_streets = gdf_streets[gdf_streets['geometry'].astype(str) != 'LINESTRING EMPTY'] gdf_streets_by_region = gdf_streets_by_region.append(gdf_streets)
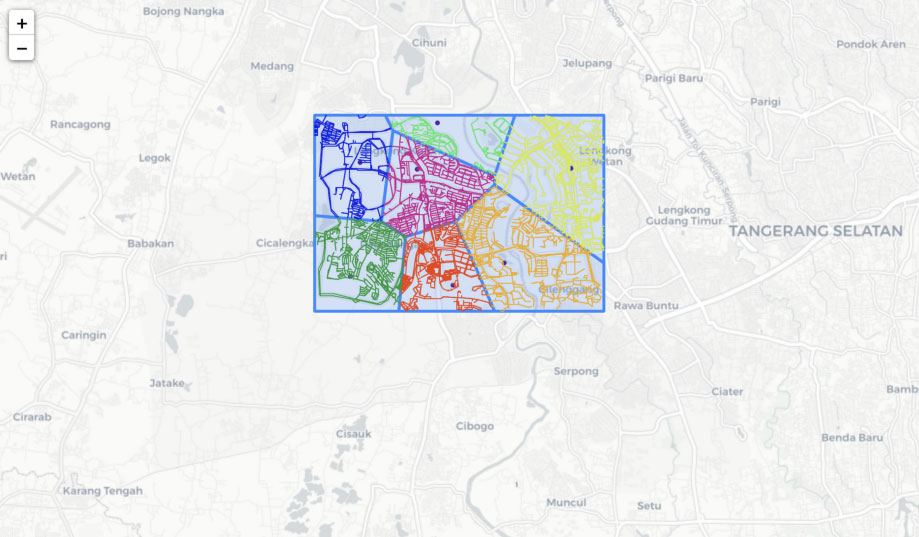
A continuación se muestra la visualización de las regiones de Voronoi en el mapa.
¡El mapa se ve genial! Desafortunadamente, aún no está listo para usarse en aplicaciones de la vida real, el problema son estas regiones de Voronoi creadas usando la distancia euclidiana en lugar de la distancia de la red.
Espero que hayas disfrutado leyendo este artículo. Para obtener más detalles del código, simplemente haga clic en este enlace.







Añadir comentario