Guía más sencilla para los supuestos del análisis de regresión

Hola, les saluda Luis y para hoy les traigo otro nuevo tutorial.

La regresión lineal es la relación no trivial más simple. ¡El mayor error que se puede cometer es realizar un análisis de regresión que viola uno de sus supuestos!

Por lo tanto, es importante considerar estos supuestos antes de aplicar el análisis de regresión al conjunto de datos.

Linealidad: el modelo especificado debe representar una relación lineal

Este es el supuesto más simple de tratar, ya que significa que la relación entre la variable dependiente y la independiente es lineal, donde la variable independiente se multiplica por su coeficiente para obtener la variable dependiente.

Y = β0 + β1X1 +… + βkXk + ε

Es bastante fácil verificar este supuesto, ya que trazar una variable independiente contra una variable dependiente en un diagrama de dispersión nos da una idea de si el patrón formado se puede representar a través de una línea o no.

Sin embargo, aplicar regresión lineal a los datos no sería apropiado si una línea no se ajusta a los datos. En el último caso, se puede realizar una regresión no lineal, una transformación logarítmica o exponencial en el conjunto de datos para convertirlo en una relación lineal.

Sin endogeneidad de regresores: las variables independientes no deben correlacionarse con el término de error

Esto se refiere a la prohibición de vinculación entre la variable independiente y el término de error. Matemáticamente, se puede expresar de la siguiente manera.

𝜎 𝑥, 𝜀 = 0: ∀𝑥, 𝜀

Como sabemos, las variables independientes involucradas en el modelo están algo correlacionadas. La exclusión incorrecta de una o más variables independientes que podrían ser relevantes para el modelo nos da el sesgo de la variable omitida.

Esta variable excluida finalmente se refleja en el término de error, lo que resulta en la covarianza entre la variable independiente y el término de error como distinto de cero.

La única forma de lidiar con este supuesto es probar diferentes variables para el modelo a fin de garantizar que las variables relevantes estén muy bien clasificadas en el modelo.

Normalidad y homocedasticidad: la varianza de los errores debe ser coherente entre las observaciones

Esta suposición establece que el término de error se distribuye normalmente y un valor esperado (media) es cero. Es importante señalar que la distribución normal del término solo se requiere para hacer inferencias.

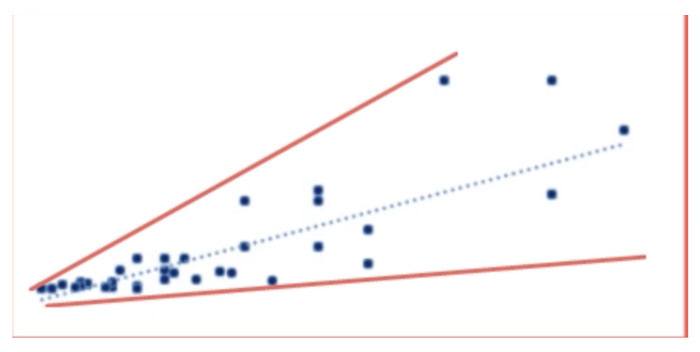
𝜀 ~ 𝑁 (0, 𝜎2)

En lo que respecta a la homocedasticidad, simplemente significa que la varianza de todos los términos de error relacionados con las variables independientes es igual entre sí. Sin embargo, a continuación se muestra un ejemplo de un conjunto de datos con diferentes variaciones de los términos de error.

La regresión realizada en este conjunto de datos tendría un mejor resultado para valores más pequeños de variables independientes y dependientes.

El camino a seguir para validar esta suposición es buscar sesgos de variables omitidas, valores atípicos y realizar una transformación logarítmica.

Sin autocorrelación: no debe existir una relación identificable entre los valores del término de error

Esta suposición es la menos favorita de todas, ya que es difícil de solucionar. Matemáticamente, se representa de la siguiente manera.

𝜎 𝜀𝑖𝜀𝑗 = 0: ∀𝑖 ≠ 𝑗

Se supone que los términos de error no están correlacionados. Una forma común de identificar esto es la prueba de Durbin-Watson, que se proporciona en la tabla de resumen de regresión.

Si el valor es menor que uno o más de tres, indica autocorrelación. Si el valor es 2, no hay autocorrelación. Es mejor evitar la regresión lineal cuando hay autocorrelación.

Sin multicolinealidad: Ninguna variable predictora debe ser perfectamente (o casi perfecta) explicada por los otros predictores

Se observa cuando dos o más variables tienen alta correlación. La lógica detrás de esta suposición es que si dos variables tienen alta colinealidad, no tiene sentido representar ambas variables en el modelo.

𝜌 𝑥𝑖𝑥𝑗 ≉1: ∀𝑖, 𝑗; 𝑖 ≠ 𝑗

Es fácil validar esta suposición descartando una de las variables o transformándolas en una.

Las críticas / sugerencias son bienvenidas 🙂.