Bienvenido, soy Miguel y hoy les traigo un tutorial.
Recientemente me enfrenté a un problema en el que tuve que buscar de manera eficiente ubicaciones que están geográficamente cerca de un punto específico. Como el enfoque ingenuo, que incluye calcular una distancia entre docenas de pares de puntos, no me parece tan eficiente, investigué un poco y probé la implementación del árbol R proporcionada por Apple desde GameKit.
Esta historia es una inmersión rápida en los conceptos básicos de R-tree y presenta un breve ejemplo de uso de GKRTree proporcionado por Apple.
Índice
Conceptos básicos del árbol R
R-tree es una estructura de datos que tiene una amplia aplicación para indexar datos espaciales. El concepto fue propuesto por primera vez por Antonin Guttman en 1984. La idea clave detrás del árbol R es agrupar los objetos cercanos y representarlos con sus rectángulos o cajas delimitadores mínimos. El rectángulo delimitador mínimo, a menudo denominado MBR, es el rectángulo más pequeño que contiene un grupo determinado de objetos. Los MBR de los MBR de grupo de nivel superior de los nodos secundarios. Eso hace que las búsquedas en el árbol sean eficientes, ya que la consulta que no se cruza con el rectángulo delimitador en un nivel superior tampoco puede cruzar ninguno de los MBR de los objetos contenidos. Eso hace que el filtrado de elementos no coincidentes sea más rápido.
Para tener una mejor imagen de cómo están estructurados los datos, echemos un vistazo a ese diagrama de Wikipedia. Podemos ver regiones marcadas en negro de nivel superior que cubren las partes más grandes de la superficie y contienen áreas azules más pequeñas. Podemos observar que cuando buscamos un elemento que se encuentra dentro del cuadro R15, podemos filtrar todos los elementos secundarios R1 en una sola comparación, lo que reduce significativamente la cantidad de cálculo necesario para una operación de búsqueda.
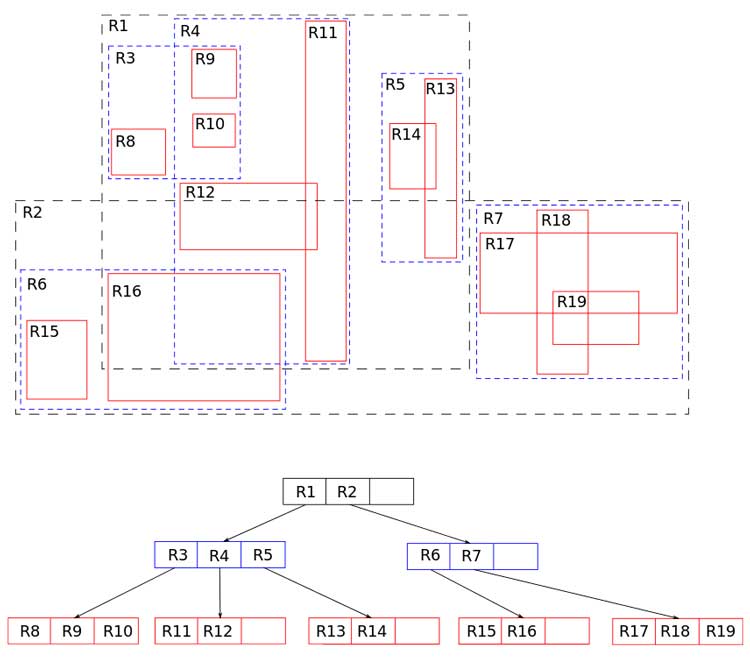
R-tree también es un árbol de búsqueda equilibrado, lo que significa que todas las hojas están en el mismo nivel. Además, esa estructura también está optimizada para el almacenamiento en disco, por lo que encontró una amplia aplicación en el campo de la base de datos.
Los árboles R pueden ser útiles para muchas tareas:
- Encontrar PDI que se encuentran a una cierta distancia de una ubicación determinada
- Decidir qué objetos del juego están lo suficientemente cerca como para desencadenar interacciones
- Buscando nodos más cercanos en la cuadrícula de coordenadas
- Y muchos más…
Árbol R en Swift
GKRTree es una implementación del concepto de árbol R proporcionado por Apple en GameKit. Como soy más bien un tipo de persona que se basa en implementaciones profundamente probadas y probadas en batalla, en lugar de implementar una yo mismo, lo intenté en mi caso de uso.
Supongamos que nuestros datos son ubicaciones representadas por la siguiente clase. Es necesario que un objeto que sea un elemento GKRTree sea subclases de NSObject.
class SomeLocation: NSObject {
let boundingBoxSize: Float = 0.1
let name: String
let x: Float
let y: Float
init(name: String, x: Float, y: Float) {
self.name = name
self.x = x
self.y = y
super.init()
}
}
Para crear una instancia de GKRTree, es necesario especificar la capacidad máxima. Luego, especifiquemos un par de instancias de ubicación y creemos un objeto GKRTree.
let sampleLocations = [
SomeLocation(name: "A", x: 1.0, y: 1.0),
SomeLocation(name: "B", x: 3.0, y: 3.0),
SomeLocation(name: "C", x: 3.0, y: 2.0)
]
let rTree = GKRTree(maxNumberOfChildren: sampleLocations.count)
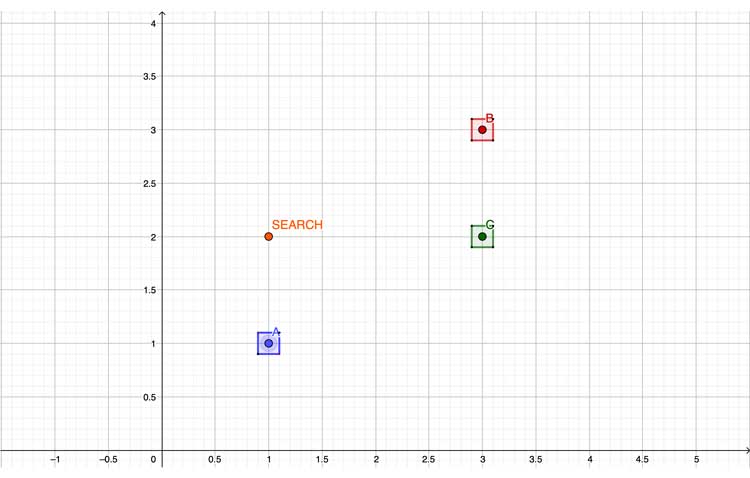
Nuestros puntos se pueden dibujar usando el diagrama a continuación, que puede ser útil para visualizar las relaciones espaciales entre ellos.

Una vez que tenemos una instancia de árbol R y los elementos creados, es hora de ponerlos en la estructura real. La API para eso se ve como sigue
func addElement(_ element: ElementType,
boundingRectMin: vector_float2,
boundingRectMax: vector_float2,
splitStrategy: GKRTreeSplitStrategy)
Toma un elemento con sus coordenadas mínimas y máximas de cuadro delimitador. Al igual que en nuestro escenario, estamos utilizando puntos como ubicaciones que necesitamos traducir de alguna manera en cuadros delimitadores que están siendo aceptados por la API de GKRTree. Podemos lograr eso simplemente agregando algo de relleno a sus coordenadas. Podemos hacerlo agregando variables calculadas a la clase SomeLocation.
class SomeLocation: NSObject {
let boundingBoxSize: Float = 0.1
...
var boundingBoxMin: vector_float2 {
vector_float2(x-boundingBoxSize, y-boundingBoxSize)
}
var boundingBoxMax: vector_float2 {
vector_float2(x+boundingBoxSize, y+boundingBoxSize)
}
}
Los rellenos que acabamos de agregar ahora se pueden visualizar en el diagrama.

Ahora podemos agregar los elementos al árbol.
sampleLocations.forEach { location in
rTree.addElement(location,
boundingRectMin: location.boundingBoxMin,
boundingRectMax: location.boundingBoxMax,
splitStrategy: .reduceOverlap)
}
El último parámetro utilizado al agregar elementos es el splitStrategy. Define cómo el árbol reorganiza su estructura interna. Se pueden aplicar cuatro estrategias diferentes. El resultado general depende de la organización de los datos que procesa, por lo que es valioso verificar diferentes estrategias y comparar el rendimiento para elegir la más eficiente.
Ahora es el momento de buscar los vecinos más cercanos para un punto seleccionado. Supongamos que estará en (1,2). Al observar el método de búsqueda de GKRTree, podemos ver que acepta, de manera similar al utilizado para agregar elementos, los límites del cuadro delimitador.
func elements(inBoundingRectMin rectMin: vector_float2, rectMax: vector_float2) -> [ElementType]
Eso nos lleva a especificar el área en la que queremos encontrar puntos.
let searchPosition = SomeLocation(name: "S", x: 1.0, y: 2.0)
let searchBoxSize: Float = 1.5
let searchBoxMin = vector_float2(searchPosition.x - searchBoxSize,
searchPosition.y - searchBoxSize)
let searchBoxMax = vector_float2(searchPosition.x + searchBoxSize,
searchPosition.y + searchBoxSize)
El cuadro delimitador de búsqueda también se puede agregar a nuestro diagrama. Como podemos ver a continuación, deberíamos esperar recuperar una ubicación ya que solo hay un elemento que cae en el cuadro delimitador que acabamos de definir.
También podemos observar que modificar los criterios de búsqueda aumentando el tamaño del cuadro nos da más resultados que luego pueden ser ordenados, filtrados y procesados dependiendo del caso de uso real.
let results = rTree.elements(inBoundingRectMin: searchBoxMin, rectMax: searchBoxMax)
Al usar R-tree, vale la pena tener en cuenta que esta estructura de datos opera de una manera que mantiene el árbol equilibrado. Significa que ninguna rama del árbol R contiene significativamente más objetos o subramas que cualquier otra rama. Da como resultado un aumento de la cantidad de tiempo necesario para realizar operaciones de inserción y eliminación, al tiempo que reduce el tiempo necesario para buscar elementos.
Ejemplo completo
El código completo del ejemplo analizado tiene el siguiente aspecto.
import GameKit
class SomeLocation: NSObject {
let boundingBoxSize: Float = 0.1
let name: String
let x: Float
let y: Float
init(name: String, x: Float, y: Float) {
self.name = name
self.x = x
self.y = y
super.init()
}
var boundingBoxMin: vector_float2 {
vector_float2(x-boundingBoxSize, y-boundingBoxSize)
}
var boundingBoxMax: vector_float2 {
vector_float2(x+boundingBoxSize, y+boundingBoxSize)
}
}
let sampleLocations = [
SomeLocation(name: "A", x: 1.0, y: 1.0),
SomeLocation(name: "B", x: 3.0, y: 3.0),
SomeLocation(name: "C", x: 3.0, y: 2.0)
]
let rTree = GKRTree(maxNumberOfChildren: sampleLocations.count)
sampleLocations.forEach { location in
rTree.addElement(location,
boundingRectMin: location.boundingBoxMin,
boundingRectMax: location.boundingBoxMax,
splitStrategy: .reduceOverlap)
}
let searchPosition = SomeLocation(name: "A", x: 1.0, y: 2.0)
let searchBoxSize: Float = 1.5
let searchBoxMin = vector_float2(searchPosition.x - searchBoxSize,
searchPosition.y - searchBoxSize)
let searchBoxMax = vector_float2(searchPosition.x + searchBoxSize,
searchPosition.y + searchBoxSize)
let results = rTree.elements(inBoundingRectMin: searchBoxMin, rectMax: searchBoxMax)
Conclusión
Los árboles R son una estructura de datos ampliamente aplicada que se puede utilizar para implementar varios tipos de búsquedas de datos espaciales. Para las plataformas de Apple, hay una implementación incorporada proporcionada en el marco de GameKit que hace que la implementación de la búsqueda en datos espaciales sea realmente rápida. Si necesita un equivalente en 3D, asegúrese de verificar GKOctree.
Espero que el ejemplo presentado sea una base útil para implementar sus propias soluciones.
¡Gracias por leer!








Añadir comentario