Numpy al descubierto: una guía para principiantes sobre estadísticas con Numpy

Muchas empresas que contratan para puestos de Python requieren específicamente conocimientos de la biblioteca Numpy.

NumPy es una biblioteca de Python que se utiliza para trabajar con matrices. También tiene funciones para trabajar en el dominio de  álgebra lineal, transformada de Fourier y matrices .

NumPy fue creado en 2005 por Travis Oliphant. Es un proyecto de código abierto y puedes usarlo libremente. NumPy son las siglas de Numerical Python.

En Python tenemos listas que sirven como matrices, pero son lentas de procesar. NumPy tiene como objetivo proporcionar un objeto de matriz que sea  hasta 50 veces más rápido  que las listas tradicionales de Python.

El objeto de matriz en NumPy se llama ndarray, proporciona muchas funciones de apoyo que hacen que trabajar con ndarray muy fácil.

Las matrices se utilizan con mucha frecuencia en la ciencia de datos, donde la velocidad y los recursos son muy importantes.

 Los resultados del aprendizaje: 

Media:

Antes de usar Numpy en un conjunto de datos, debemos convertirlo en una matriz. Array en Python es similar a la lista en Python.

Está representado por llaves con valores en su interior separados por comas. Para realizar operaciones de matriz en una lista,  primero debemos transformarla en matriz .

Ejemplo:

survey_responses = [5, 10.2, 4, .3,6.6]

Luego podemos transformar el conjunto de datos en una matriz NumPy usando

survey_array = np.array (survey_responses)

A tener en cuenta: np es un alias de Numpy

Media de cálculo

survey_mean = np.mean (survey_array)

Salida:

Matrices 0-D

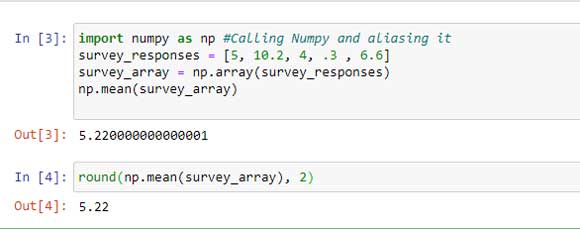
Las matrices 0-D, o escalares, son los elementos de una matriz. Cada valor de una matriz es una matriz 0-D.

Por ejemplo: arr = np.array (42)

Matrices 1-D

Una matriz que tiene matrices 0-D como sus elementos se denomina matriz unidimensional o 1-D. Estos son los arreglos más comunes y básicos.

Por ejemplo: arr = np.array ([1, 2, 3, 4, 5])

Matrices 2-D

Una matriz que tiene matrices 1-D como sus elementos se denomina matriz 2-D. A menudo se utilizan para representar tensores de matriz o de segundo orden.

Por ejemplo: arr = np.array ([[1, 2, 3], [4, 5, 6]])

Matrices 3-D

Una matriz que tiene matrices 2-D (matrices) como sus elementos se llama matriz 3-D. A menudo se utilizan para representar un tensor de tercer orden.

Por ejemplo: arr = np.array ([[[1, 2, 3], [4, 5, 6]] [[1, 2, 3], [4, 5, 6]]])

Matrices nD

Una matriz que tiene matrices (n-1) -D como sus elementos se llama matriz nD.

Verificar el número de dimensiones de una matriz

NumPy Arrays proporciona la ndim atributo que devuelve un número entero que nos dice cuántas dimensiones tiene la matriz.

Creación de matrices de dimensiones superiore

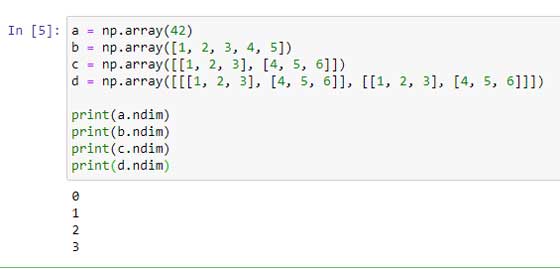
Una matriz puede tener cualquier número de dimensiones.

Cuando se crea la matriz, puede definir el número de dimensiones utilizando el ndmin argumento.

Por ejemplo: arr = np.array ([1, 2, 3, 4], ndmin = 5)

nota: Para buscar dimensiones se usa «ndim» mientras que para crear dimensiones se usa «ndmin». Ambos no deben confundirse para ser iguales.

Problema de ejemplo 4 partes

ensayos_allergias = np.array ([[6, 1, 3, 8, 2], [2, 6, 3, 9, 8], [5, 2, 6, 9, 9]])

Salida:

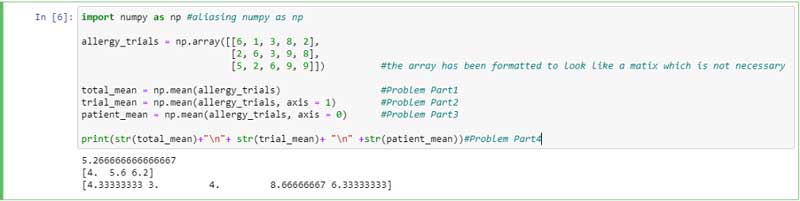
Pregunta

¿Qué es un eje en Numpy?

Responder

Un eje es similar a una dimensión. Para una matriz bidimensional, hay 2 ejes:  vertical y horizontal .

Al aplicar ciertas funciones de Numpy como np.mean(), podemos especificar en qué eje queremos calcular los valores.

Outliers

Como podemos ver, la media es una forma útil de comprender rápidamente diferentes partes de nuestros datos. Sin embargo, la media está muy influenciada por los valores específicos de nuestro conjunto de datos. ¿Qué sucede cuando uno de esos valores es significativamente diferente del resto?

Los valores que no se ajustan a la mayoría de un conjunto de datos se conocen como  valores atípicos . Es importante identificar valores atípicos porque si pasan desapercibidos, pueden sesgar nuestros datos y dar lugar a errores en nuestro análisis (cómo determinar la media). También pueden ser útiles para señalar errores en nuestra recopilación de datos.

Cuando somos capaces de identificar valores atípicos, podemos determinar si se debieron a un error en la recolección de la muestra o si representan o no una desviación significativa pero real de la media.

Clasificación y valores atípicos

Una forma de identificar rápidamente los valores atípicos es ordenando nuestros datos. Una vez ordenados nuestros datos, podemos echar un vistazo rápidamente al principio o al final de una matriz para ver si algunos valores se encuentran mucho más allá del rango esperado. Podemos usar la función NumPy np.sort para ordenar nuestros datos.

Tomemos el ejemplo de la altura de un estudiante de tercer grado e imaginemos que un estudiante de octavo grado entró en nuestro experimento:

>>> heights = np.array([49.7, 46.9, 62, 47.2, 47, 48.3, 48.7])

Si usamos np.sort, podemos identificar inmediatamente al estudiante más alto ya que su altura (62 ”) está notablemente fuera del rango del conjunto de datos:

>>> np.sort(heights)
array([ 46.9, 47. , 47.2, 48.3, 48.7, 49.7, 62])

Ordenación inversa: para cualquier matriz dada podemos invertir el orden de los elementos mediante np.sort (array_name[::-1])

Mediana

Otra métrica clave que podemos usar en el análisis de datos es la mediana. La mediana es el valor medio de un conjunto de datos que se ordenó en términos de magnitud (de menor a mayor).

Veamos la siguiente matriz:

np.array( [1, 1, 2, 3, 4, 5, 5])

En este ejemplo, la mediana sería 3, porque se encuentra a medio camino entre el valor mínimo y el valor máximo.

Si la longitud de nuestro conjunto de datos fuera un número par, la mediana sería el valor a medio camino entre los dos valores centrales. Entonces, en el siguiente ejemplo, la mediana sería 3,5:

np.array( [1, 1, 2, 3, 4, 5, 5, 6])

Pero, ¿y si tuviéramos un conjunto de datos muy grande? Sería muy tedioso contar todos los valores. Afortunadamente, NumPy también tiene una función para calcular la mediana, np.median:

>>> my_array = np.array([50, 38, 291, 59, 14])
>>> np.median(my_array)
50.0

Media vs mediana

En un conjunto de datos, el valor de la mediana puede proporcionar una comparación importante con la media. A diferencia de una media, la mediana no se ve afectada por valores atípicos. Esto se vuelve importante en conjuntos de datos asimétricos, conjuntos de datos cuyos valores no se distribuyen de manera uniforme.

Percentiles

Como sabemos, la mediana es la mitad de un conjunto de datos: es el número para el cual el 50% de las muestras están por debajo y el 50% de las muestras por encima. Pero, ¿y si quisiéramos encontrar un punto en el que el 40% de las muestras estén por debajo y el 60% de las muestras por encima? 

Este tipo de punto se llama percentil. El percentil N se define como el punto N% de las muestras que se encuentran por debajo de él.

Entonces, el punto donde el 40% de las muestras están por debajo se llama el percentil 40. Los percentiles son medidas útiles porque pueden decirnos dónde se encuentra un valor particular dentro del conjunto de datos mayor.

Veamos la siguiente matriz:

d = [1, 2, 3, 4, 4, 4, 6, 6, 7, 8, 8]

Hay 11 números en el conjunto de datos. El percentil 40 tendrá el 40% de los 10 números restantes debajo de él (el 40% de 10 es 4) y el 60% de los números arriba (60% de 10 es 6). Entonces, en este ejemplo, el percentil 40 es 4.

En NumPy, podemos calcular percentiles usando la función np.percentile, que toma dos argumentos: la matriz y el percentil para calcular.

Así es como usaríamos NumPy para calcular el percentil 40 de la matriz d:

>>> d = np.array([1, 2, 3, 4, 4, 4, 6, 6, 7,  8, 8])
>>> np.percentile(d, 40)
4.00

Algunos percentiles tienen nombres específicos:

El mínimo, el primer cuartil, la mediana, el tercer cuartil y el máximo de un conjunto de datos se denominan resumen de cinco números. Este conjunto de números es muy bueno para calcular cuando obtenemos un nuevo conjunto de datos.

La diferencia entre el primer y el tercer cuartil es un valor llamado rango intercuartil. Por ejemplo, digamos que tenemos la siguiente matriz:

d = [1, 2, 3, 4, 4, 4, 6, 6, 7, 8, 8]

Podemos calcular los percentiles 25 y 75 usando np.percentile:

np.percentile(d, 25)
>>> 3.5
np.percentile(d, 75)
>>> 6.5

Luego, para encontrar el rango intercuartílico, restamos el valor del percentil 25 del valor del 75:

6.5 - 3.5 = 3

El 50% del conjunto de datos estará dentro del rango intercuartílico. El rango intercuartil nos da una idea de cuán dispersos están nuestros datos. Cuanto menor sea el valor del rango intercuartílico, menor será la varianza en nuestro conjunto de datos. Cuanto mayor sea el valor, mayor será la varianza.

Desviación Estándar

Cuando la desviación estándar es pequeña, los valores estarán menos dispersos y estarán más cerca de la media. Esto hará que la forma general de este conjunto de datos parezca menos caótica y más nivelada.

Cuando la desviación estándar es grande, los valores estarán más separados de la media. La forma del conjunto de datos parecerá más desigual y caótica a medida que aumenta la desviación estándar.

Podemos encontrar la desviación estándar de un conjunto de datos usando la función Numpy np.std:

>>> nums = np.array([65, 36, 52, 91, 63, 79])
>>> np.std(nums)
17.716909687891082

Espero que te haya servido, gracias por leer.