Hola, me llamo Miguel y aquí les traigo otro post.
Cómo reconocen las computadoras los patrones
El término aprendizaje automático puede parecer provocativo. Las máquinas no aprenden como los humanos. Sin embargo, cuando se les asignan tareas identificables para completar, las máquinas sobresalen.
Los algoritmos responden preguntas. Una vez capacitados, obtienen información relevante y dan una suposición fundamentada a su pregunta.
Supongamos que trabaja para una empresa de publicidad que quiere identificar un público objetivo para artículos de lujo. La empresa no se molestará en hacer publicidad a la mayoría de los consumidores. Entonces, la empresa decide que quiere estimar los salarios en Topeka, Kansas, para encontrar objetivos adecuados para su campaña de marketing. La empresa encuentra un conjunto de datos en línea sobre los residentes locales. Estos datos se componen de horas trabajadas mensualmente, edad y salario mensual. La empresa espera utilizar este conjunto de datos para predecir el salario de los consumidores que no están dentro del conjunto de datos.
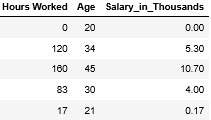
Salario mensual
Estos primeros cinco ejemplos contienen ejemplos mensuales de información descriptiva y salarios.
Parece que hay un patrón en estos datos. Intuitivamente, si alguien trabaja más horas se le paga más. También tiene sentido que los trabajadores mayores ganen más debido a su experiencia.
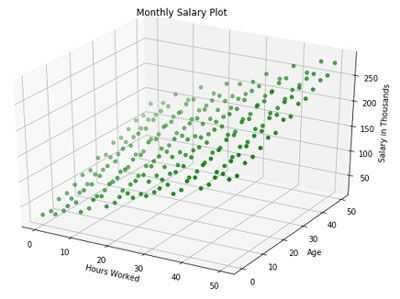
Echemos un vistazo más de cerca a todo el conjunto de datos. Surge un patrón: tanto la edad como las horas trabajadas aumentan el salario.
Por cada hora trabajada, el salario en promedio aumenta en una cierta cantidad. Por cada año de edad, el salario aumenta en promedio en alguna otra cantidad. La fórmula de esta relación se ve así:
A + (Horas trabajadas * B) + (Edad * C) = Salario
Donde A, B y C son variables desconocidas.
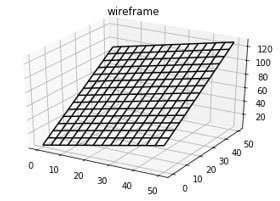
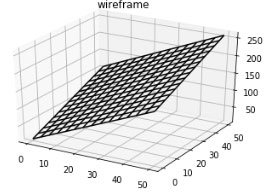
Para cada A, B y C existe un plano único.
Tomemos la lista de <A, B, C> y llamémosla θ. Luego, escojamos un número aleatorio para cada uno. Esto crea un avión.
Este plano es como la fórmula en negrita. Toma dos números y devuelve Z. Dependiendo de los tres números de Theta, el avión toma una forma diferente.
Usemos este plano generado aleatoriamente como una ecuación para los datos de los salarios. Para cada fila del conjunto de datos creamos una única predicción.
Ahora estableceremos un punto de referencia para el desempeño de la predicción. Tomemos la diferencia entre la predicción y las columnas de salarios reales, cuadrando cada número, y sumémoslos:
Cost(Salary_in_Thousands, Predicted Salary) = Sum((Salary_in_Thousands-Predicted Salary)²)
Este punto de referencia para el rendimiento se llama función de costo o función de pérdida. Cuanto mayor sea la suma, mayor será la distancia entre las predicciones y los salarios reales.
Dependiendo de la ubicación de θ el modelo será más o menos preciso. Para minimizar la función de coste tendremos que ajustar los valores de θ.
La pregunta sigue siendo: ¿en qué dirección nos movemos θ?
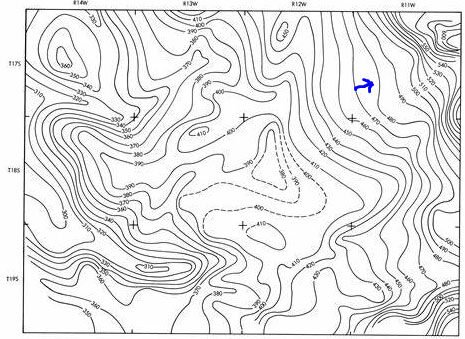
Los mapas de contorno muestran la elevación usando líneas de contorno. A lo largo de estas líneas la elevación es igual. Perpendicularmente a esto está la línea de mayor pendiente, llamada gradiente. Moverse en esta dirección aumenta el valor de Z más rápidamente. Al moverse en la dirección opuesta, el valor de Z disminuye más rápido.
Usaremos la misma idea para disminuir el error en nuestro modelo de salario. Primero, calculamos el error en función de θ.
Luego actualizamos θ usando la siguiente fórmula:
θ = θ-∇Cost() … donde ∇Cost() es el gradiente.
Al restar el gradiente disminuimos la función de costo global y encontramos un mejor θ. Debido a que estamos restando el gradiente este método se llama Gradient Descent.
Con nuestro nuevo θ calculamos las nuevas predicciones. Luego calculamos el nuevo costo y el nuevo gradiente. Esto nos lleva al siguiente ciclo.
Una vez que el costo es lo suficientemente bajo, mantenemos θ como nuestro modelo final. Por ejemplo, si el costo no disminuye por tres bucles rectos, podemos detener el proceso.
Usaremos el modelo final para predecir los salarios de los consumidores en Topeka, Kansas usando las edades y la carga de trabajo de los consumidores. Si nuestro modelo predice un salario lo suficientemente alto, lo marcaremos como el público objetivo para los anuncios de nuestra marca de lujo.
Aquí está nuestro modelo final.
Teniendo en cuenta los datos originales, es una fuerte aproximación al patrón subyacente.
Este es un gráfico que representa nuestro modelo.
La izquierda representa las entradas del modelo: edad y horas trabajadas.
Los datos se mueven de izquierda a derecha a través de tres canales. Cuanto más amplio sea el canal, indicado por θ[i], mayor será la salida a la derecha. La línea superior representa 1*θ[0]
El lado derecho es la salida del modelo. Es la suma de cada entrada multiplicada por su θ.
Las matemáticas se escriben como <1, edad, horas trabajadas>*θ = Predicción del salario.












Añadir comentario