Algoritmos desde cero: Máquinas vectoriales de soporte

Bienvenido, les saluda Luis y aquí les traigo este tutorial.

Detallar y construir una máquina de vectores de soporte desde cero

Un algoritmo popular que es capaz de realizar clasificaciones y regresiones lineales o no lineales, Support Vector Machines fue la comidilla de la ciudad antes del surgimiento del aprendizaje profundo debido al emocionante truco del kernel: si la terminología no tiene sentido para usted en este momento, don No te preocupes por eso. Al final de esta publicación, comprenderá bien la intuición de las SVM, lo que sucede bajo el capó de las SVM lineales y cómo implementar una en Python.

Intuición

En los problemas de clasificación, el objetivo de la SVM es ajustar el mayor margen posible entre las 2 clases. Por el contrario, la tarea de regresión invierte el objetivo de la tarea de clasificación e intenta encajar tantas instancias como sea posible dentro del margen. Primero nos centraremos en la clasificación.

Si nos enfocamos únicamente en los extremos de los datos (las observaciones que están en los bordes del clúster) y definimos un umbral como el punto medio entre los dos extremos, nos queda un margen que usamos para separar el dos clases: esto a menudo se denomina hiperplano. Cuando aplicamos un umbral que nos da el margen más grande (lo que significa que somos estrictos para asegurarnos de que ninguna instancia aterrice dentro del margen) para hacer clasificaciones, esto se llama Clasificación de margen duro (algunos textos se refieren a esto como Clasificación de margen máximo).

Cuando se detalla la clasificación de margen estricto, siempre ayuda ver lo que está sucediendo visualmente, por lo tanto, la Figura 2 es un ejemplo de clasificación de margen estricto. Para hacer esto usaremos el conjunto de datos de iris de scikit-learn y función de utilidad plot_svm() que puede encontrar cuando accede al código completo en github – enlace.

A tener en cuenta:: Esta historia se escribió directamente desde los cuadernos de jupyter utilizando el paquete python jupyter_to_manualestutor – para obtener más información sobre este paquete haga clic aquí – y la versión comprometida en github es un primer borrador, por lo que es posible que notes algunas alteraciones en esta publicación.

import pandas as pd 
import numpy as np 
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt 
%matplotlib inline# store the data 
iris = load_iris()

# convert to DataFrame
df = pd.DataFrame(data=iris.data,
columns= iris.feature_names)

# store mapping of targets and target names
target_dict = dict(zip(set(iris.target), iris.target_names))

# add the target labels and the feature names
df["target"] = iris.target
df["target_names"] = df.target.map(target_dict)

# view the data
df.tail()

Figura 1: Conjunto de datos original

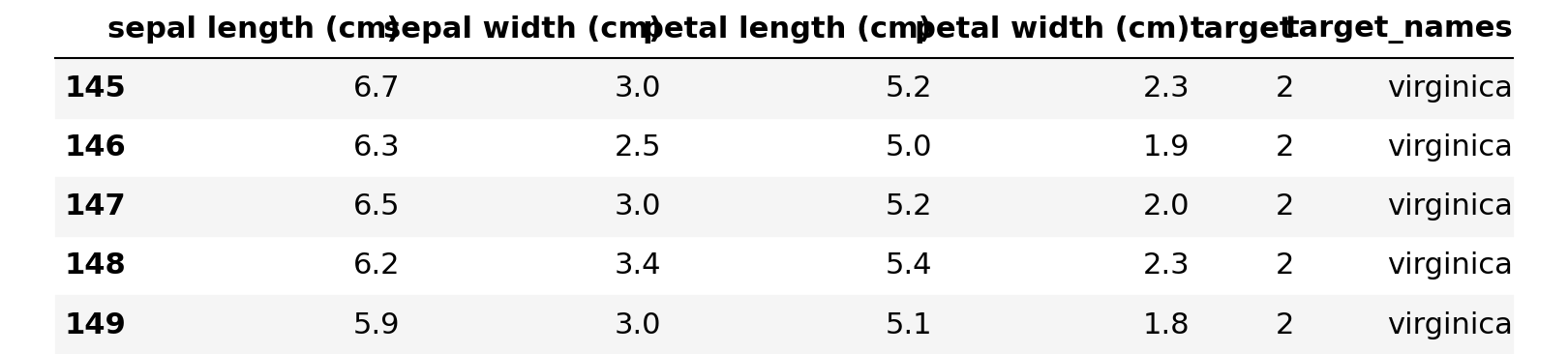
# setting X and y  
X = df.query("target_names == 'setosa' or target_names == 'versicolor'").loc[:, "petal length (cm)":"petal width (cm)"] 
y = df.query("target_names == 'setosa' or target_names == 'versicolor'").loc[:, "target"]

# fit the model with hard margin (Large C parameter)
svc = LinearSVC(loss="hinge", C=1000)
svc.fit(X, y)

plot_svm()

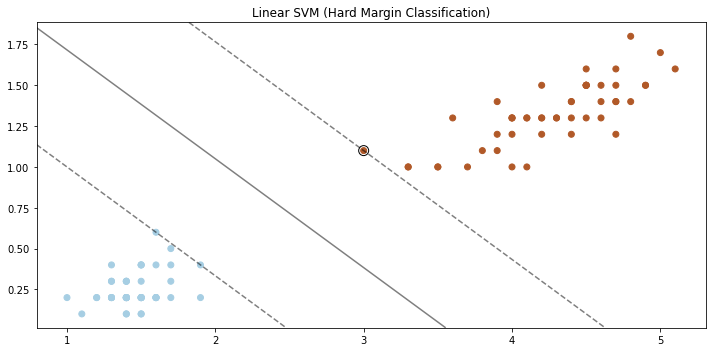
La Figura 2 muestra cómo Linear SVM usa la clasificación de margen rígido para garantizar que ninguna instancia se encuentre dentro del margen. Aunque esto se ve bien para nuestro escenario actual, debemos tener cuidado de tener en cuenta las trampas que conlleva realizar una clasificación de margen estricto:

1. Muy sensible a los valores atípicos.
2. Solo funciona cuando las clases son linealmente separables.

Manejo de valores atípicos y datos no lineales

Una alternativa más flexible a la clasificación de margen estricto es la clasificación de margen flexible, que es una buena solución para superar los errores enumerados anteriormente al realizar la clasificación de margen estricto, principalmente para resolver el problema de la sensibilidad a los valores atípicos. Cuando permitimos que haya algunas clasificaciones erróneas (lo que significa que algunas observaciones negativas pueden clasificarse como positivas y viceversa), la distancia desde el umbral hasta las observaciones se denomina margen suave . En la clasificación de margen blando, nuestro objetivo es lograr un buen equilibrio entre maximizar el tamaño del margen y limitar la cantidad de violaciones en el margen (el número de observaciones que aterrizan en el margen).

Sí, los clasificadores lineales de SVM (margen rígido y margen suave) son bastante eficientes y funcionan muy bien en muchos casos, pero cuando el conjunto de datos no es separable linealmente, como suele ser el caso de muchos conjuntos de datos, una mejor solución es hacer uso del truco del kernel de las SVM (una vez que comprenda el truco del kernel, puede notar que no es exclusivo de las SVM). El truco del kernel mapea datos separables de forma no lineal en una dimensión superior y luego usa un hiperplano para separar las clases. Lo que hace que este truco sea tan emocionante es que el mapeo de los datos en dimensiones más altas en realidad no agrega las nuevas características, pero aún así obtenemos los mismos resultados que si lo hiciéramos. Dado que no tenemos que agregar las nuevas características a nuestros datos, nuestro modelo es mucho más eficiente computacionalmente y funciona igual de bien.

Verá un ejemplo de este fenómeno a continuación.

Terminología

• Límite de decisión : el hiperplano que separa el conjunto de datos en dos clases
• Vectores de soporte : las observaciones están en el borde del cúmulo (ubicado más cerca del hiperplano separador).
• Margen duro : cuando imponemos estrictamente que todas las observaciones no caen dentro del margen
• Margen suave : cuando permitimos una clasificación errónea. Buscamos encontrar un equilibrio para mantener el margen lo más grande posible y limitar el número de violaciones ( compensación de sesgo / varianza )

de sklearn.datasets importar make_moons 
de mlxtend.plotting importar plot_decision_regions 
de sklearn.preprocessing importar StandardScaler 
de sklearn.svm importar SVC# cargando los datos 
X, y = make_moons (noise = 0.3, random_state = 0) 

# scale features 
scaler = StandardScaler () 
X_scaled = scaler.fit_transform (X) 

# ajusta el modelo con kernel polinomial 
svc_clf = SVC (kernel = "poly" , grado = 3, C = 5, coef0 = 1) 
svc_clf.fit (X_scaled, y) 

# trazando las regiones de decisión 
plt.figure (figsize = (10, 5)) 
plot_decision_regions (X_scaled, y, clf = svc_clf) 

plt. show()

A tener en cuenta: Aplicamos un kernel polinomial a este conjunto de datos, sin embargo, RBF también es un kernel muy popular que se aplica en muchos problemas de Machine Learning y se usa a menudo como predeterminado cuando los datos no se pueden separar linealmente.

Creando el modelo

Ahora que hemos construido nuestra comprensión conceptual de lo que está haciendo SVM, entendamos lo que está sucediendo bajo el capó del modelo. El clasificador de SVM lineal calcula la función de decisión w.T * x + by predice la clase positiva para los resultados que son positivos o de lo contrario es la clase negativa. Entrenar un clasificador SVM lineal significa encontrar los valores wy bhacer que el margen sea lo más amplio posible mientras se evitan violaciones de márgenes (clasificación de margen duro) o se limitan (clasificación de margen suave)

La pendiente de la función de decisión es igual a la norma del vector de peso, por lo tanto, para que logremos el mayor margen posible, queremos minimizar la norma del vector de peso. Sin embargo, hay formas de hacerlo para que logremos una clasificación de margen rígido y una clasificación de margen suave.

El problema de la optimización del margen duro es el siguiente:

Y margen suave:

Implementación

A tener en cuenta: Para esta implementación, haré una clasificación de margen rígido, sin embargo, el trabajo adicional consistirá en implementaciones de Python de margen suave y el truco del kernel realizado en diferentes conjuntos de datos, incluida la tarea basada en regresión; para ser notificado de estas publicaciones, puede seguirme en Github .

from sklearn.datasets.samples_generator import make_blobs 

# generating a dataset
X, y = make_blobs(n_samples=50, n_features=2, centers=2, cluster_std=1.05, random_state=23)def initialize_param(X): 
    """
    Initializing the weight vector and bias
    """
    _, n_features = X.shape
    w = np.zeros(n_features)
    b = 0 
    return w, bdef optimization(X, y, learning_rate=0.001, lambd=0.01, n_iters=1000): 
    """
    finding value of w and b that make the margin as large as possible while
    avoiding violations (Hard margin classification)
    """
    t = np.where(y <= 0, -1, 1)
    w, b = initialize_param(X)
    
    for _ in range(n_iters): 
        for idx, x_i in enumerate(X): 
            condition = t[idx] * (np.dot(x_i, w) + b) >= 1
            if condition: 
                w -= learning_rate * (2 * lambd * w)
            else: 
                w -= learning_rate * (2 * lambd *  w - np.dot(x_i, t[idx]))
                b -= learning_rate * t[idx]
    return w, bw, b = gradient_descent(X, y)def predict(X, w, b):
    """
    classify examples
    """
    decision = np.dot(X, w) + b
    return np.sign(decision)# my implementation visualization
visualize_svm()

# convert X to DataFrame to easily copy code
X = pd.DataFrame(data=X,
                 columns= ["x1", "x2"])

# fit the model with hard margin (Large C parameter)
svc = LinearSVC(loss="hinge", C=1000)
svc.fit(X, y)

# sklearn implementation visualization
plot_svm()

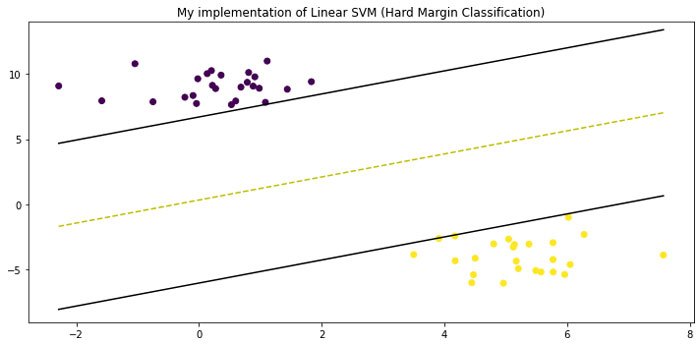
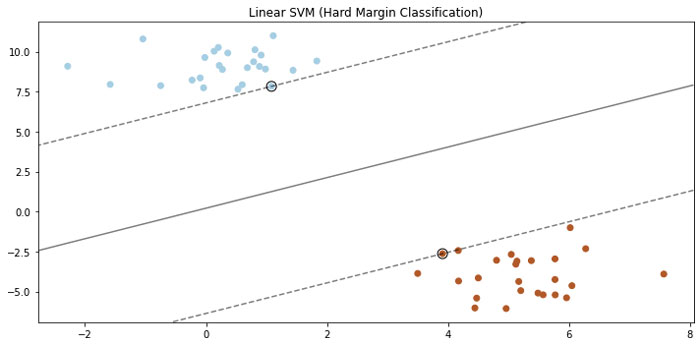
• Muy buen clasificador lineal porque encuentra el mejor límite de decisión (en un sentido de clasificación de margen duro)
• Fácil de transformar en un modelo no lineal

• No es adecuado para grandes conjuntos de datos

En conclusion