Fundamentos de las pruebas AB para todos los científicos de datos

Bienvenido, les saluda Luis y aquí les traigo un artículo.

¿Qué es la prueba de Ab?

Cuando se trata de su producto típico u organización de ingeniería, los miembros del equipo a menudo se preguntan si lo que hicieron tuvo un impacto o si la opción que eligieron entre muchas opciones de diseño diferentes fue realmente la mejor.

Dado que estas organizaciones quieren avanzar hacia una decisión de diseño basada en datos, las pruebas AB son las primeras en la fila.

La prueba AB es una metodología para comparar múltiples versiones de una función, una página, un botón, etc. mostrando las diferentes versiones a los clientes o posibles clientes y evaluando la calidad de la interacción por alguna métrica (clic, compra, después de cualquier llamada a acción, etc.).

Cada vez que desee probar múltiples variaciones de algo, es un gran caso de uso para las pruebas AB.

Cómo empezar

Es importante reducir el proceso a sus diferentes pasos.

Diseñe, planifique y ejecute su experimento

La primera parte de esto es especificar su hipótesis o lo que cree que sucederá. (Más específicamente, lo que usted cree que es la Hipótesis Alternativa y la Hipótesis NULL asume que no hay diferencia entre las variantes).

Repasemos las cosas que necesita saber o formular antes que nada:

Otro pensamiento al realizar su experimento es implementar las variantes para los clientes durante el mismo período de tiempo, en lugar de organizar diferentes variantes en diferentes períodos de tiempo.

Cuánta variación no aleatoria haya en su muestra, menos confiable será su experimento. El tiempo es un buen ejemplo de algo para estandarizar en lugar de permitir que la estacionalidad juegue un papel en el resultado de su experimento.

Cuando inicie un experimento, hágalo para todas y cada una de las variantes.

A partir de aquí, una de las preguntas más comunes que tienen las personas es ¿Cuántas muestras de cada variante necesito para tener resultados estadísticamente significativos?

Para determinar esto, realizamos algo llamado análisis de potencia. La idea del análisis de poder es identificar el tamaño de muestra requerido en función de una serie de parámetros; cosas como el poder estadístico, el valor p, el número de variantes y el tamaño de la diferencia entre la medición de los dos grupos, etc.

La razón por la que hacemos esto es para asegurarnos de que no hacemos un experimento tan largo que una tonelada de nuestros clientes tuvieron que ver la peor versión, pero aún lo suficiente para justificar nuestros resultados.

Los desglosaré aquí mismo

Carguemos el paquete pwr y usemos pwr.anova.test para identificar nuestro tamaño de muestra requerido.

He creado un par de conjuntos de datos ficticios para jugar, uno para el experimento y otro para el experimento previo.

library(pwr)
pwr.anova.test(k = 2,
n = NULL,
f = .202,
sig.level = 0.05,
power = .8)

También como referencia, incluiré un fragmento de código de lo que podría hacer para comprender la línea de base. Línea de base, siendo la variante A.

pre_experiment_data %>% 
summarize(conversion_rate = mean(call_to_action))

Como puede ver arriba, no muestra por variante es 98.

click_data %>%    
summarize(conversion_rate = mean(clicked_adopt_today))

Esto me dio el resultado de 0.502 que sirvió como base para comparar con 0.673 de la variante B.

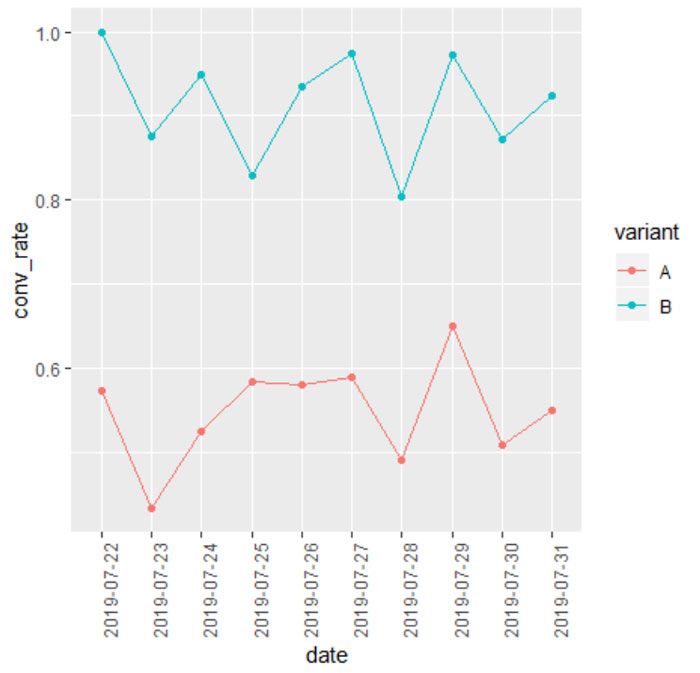
Otra opción es graficar el rendimiento de las diferentes variantes durante el transcurso del experimento. A continuación, puede ver que agrupamos los datos del experimento por fecha y variante, luego agregamos la conversión promedio.

Creo que grafica la conversión promedio por grupo a lo largo del tiempo. Como se trataba de datos de muestra, los ajusté por el bien de la visualización.

experiment_data %>%
group_by(date, variant)%>%
summarize(conv_rate = mean(call_to_action))%>%
ggplot(aes(x = date,
y = conv_rate,
color = variant,
group = variant)) +
geom_point() +
geom_line()+
theme(axis.text.x = element_text(angle = 90, hjust = 1))

Validar y analizar sus resultados

Una vez que haya recolectado una muestra de 114 por variante, es hora de validar sus resultados.

Vale la pena saltar a los datos de su experimento y revisar la tasa de conversión de su métrica agrupada por cada variante antes de pasarla a través de un glm.

experiment_data %>%
group_by(variant) %>%
summarize(conv_rate = mean(call_to_action))

Casi lo que habíamos visto anteriormente, lo cual es una buena señal.

Otra opción es el rendimiento de las diferentes variantes a lo largo del experimento.

Ahora validemos este resultado usando un GLM.

Como puede ver en la declaración a continuación, estamos tratando de interpretar el resultado de la call_to_action por el cual variant de la experiencia que tuvieron.

Ese tidy() llame al final allí simplemente limpia su salida. Para usar eso, asegúrese de descargar el paquete broom.

glm(call_to_action ~ variant,
family = "binomial",
data = experiment_data)%>%
tidy()

Primero mirando la fila para variantB puedes ver que el p.value es menor que nuestro mínimo .05.

Ahora comparando la estimación de nuestro intercept con variantB podemos ver que nuestra prueba tuvo una tasa de conversión mucho más alta que la del control.

Feliz ciencia de datos. Gracias por leer este artículo.