Bienvenido, les saluda Luis y aquí les traigo un tutorial.
Separando el teorema, sin la jerga
El teorema de Bayes es uno de los más conocidos en el campo de la probabilidad y se utiliza a menudo como modelo de referencia en el aprendizaje automático. Sin embargo, con demasiada frecuencia lo memorizan y cantan personas que no saben realmente qué P(B|E) = P(E|B) * P(B) / P(E) realmente lo hace. Este breve artículo analizará el teorema de Bayes y mostrará cómo se simplifica a una fracción intuitiva que todos usamos de manera común.
Primero, un contexto de probabilidad básico.
La creencia es una afirmación que nos gustaría verificar que sea correcta o incorrecta, como «una persona es hombre» o «una persona tiene el pelo largo». La evidencia es información conocida sobre el tema de la creencia. Por último, el | tubo vertical se utiliza como la palabra «dado …». Verás a menudo (B|E) como ‘la creencia de probabilidad B es verdadera, dada la evidencia E.’
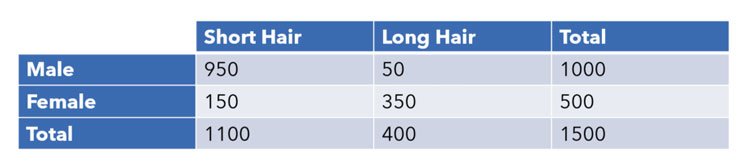
Tomemos la siguiente tabla de estudiantes de Hypothetical High School.
Queremos encontrar la probabilidad de que una persona sea mujer (creencia) dado el pelo largo (evidencia). Esto se puede expresar como (female|long hair). Incluso sin el teorema, esto es bastante sencillo de calcular de forma intuitiva. Simplemente necesitamos dividir el número de mujeres que tienen cabello largo por el número total de personas que tienen cabello largo, que es 350/400=0.875.
Vale la pena profundizar un poco en por qué tenemos esta intuición. Como sabemos que la persona tiene el pelo largo, buscamos en la columna de ‘Cabello largo’ y las dos clases dentro de esa categoría (ser hombre o mujer). Entonces, nuestra fórmula es simplemente personas que son mujeres y que tienen el cabello largo dividido por todas las personas que tienen el cabello largo.
Por lo tanto, podemos decir con seguridad que, si tienes el pelo largo, tienes un 87,5% de posibilidades de ser mujer en Hypothetical High School.
Usemos el teorema de Bayes para resolver esto, ¡y te darás cuenta de que simplemente está poniendo en términos rigurosamente matemáticos esta intuición!
Nombres de variables de a–i se utilizará para representar diferentes cantidades. Recuerda que nuestra fórmula intuitiva fue e/h, o el número de personas que son mujeres y tienen cabello largo, dividido por el número total de personas con cabello largo.
La fórmula de Bayes dice lo siguiente:
P(B|E) = P(E|B)*P(B) / P(E)
Esto se traduce en nuestro escenario a:
P(Female|Long Hair) = P(Long Hair|Female)*P(Female)/P(Long Hair)
Representemos estos usando variables. Por ejemplo, la probabilidad de que alguien tenga el pelo largo dado que es mujer es e/f, ya que e representa el número de mujeres con cabello largo y f representa el número total de mujeres. P(Female) es f/i, ya que f es el número de hembras y i es el número total de personas (hombres y mujeres).
P(Female|Long Hair) = (e/f)*(f/i) / (h/i) = (e/f)*(f/i)*(i/h)
Con una simple manipulación algebraica, nos damos cuenta de que (e/f)*(f/i) resultados en (e/i)y (e/i)*(i/h) es igual a (e/h) – ¡nuestra fórmula intuitiva!
Entonces, el Teorema de Bayes es realmente una forma indirecta de expresar una idea simple. Al menos en nuestro contexto de manipulación de fracciones, P(B) simplemente sirve como un puente para cancelar los recíprocos. Entonces, cuando use el teorema de Bayes para calcular P(B|E), esencialmente está calculando lo siguiente:
# items that are B and E / total # items that are E
El teorema de Bayes es útil para calcular esta probabilidad si es difícil o espinoso calcularla directamente haciendo uso de otras probabilidades más accesibles. Esto puede ser útil cuando calcular tres probabilidades distintas es menos costoso que calcular una primaria.
En un nivel superior, uno puede inclinarse a decir que el teorema de Bayes revela relaciones en la naturaleza de la probabilidad. A un nivel más bajo, y quizás más práctico, el teorema de Bayes es una forma inteligente de sortear el cálculo directo de una probabilidad con otras probabilidades y la multiplicación en cadena.
Gracias por leer.

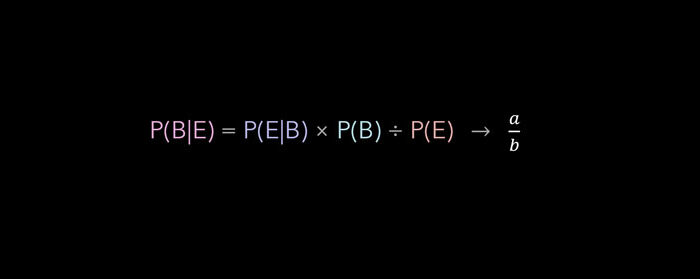







Añadir comentario